Polynomials Exercise 2.1 and 2.2

Welcome to Gurukul with Arya Gautam

Polynomials

Mathematics Class Tenth

• Exercise 2.1 and 2.2

   

What is a Polynomial? NCERT Exercise 2.1 and 2.2

An expression which consists variables and coefficient and non-negative integer components involving operations of addition, subtraction and multiplication only is called POLYNOMIAL.

Example:

$x^2+4x-7$, $x^3+2x^{2}y-y+1$, $3x$, 5, etc.

On the other hand $x^{-2}y$, $\frac{1}{x}$, $\frac{2}{x+1}$, $\sqrt{x}$, etc. are not polynomials. Because a polynomial cannot have

(i) an exponent with negative sign , such as $-2$, $-5$, etc.

(ii) no any term in a polynomial can be dividing by a variable, such as $\frac{1}{x}$

(iii) an exponent with fractional exponent, such as $\sqrt{x}$ as it is written as $x^{\frac{1}{2}}$

A Polynomial can have constants, variables, and exponents.

Examples of

Constants: $3,2,-2,\frac{1}{4}$ etc.

Variables: $x,yx,z,abc$, etc.

Exponents: $0,1,2,3,4$, etc.

Degree of Polynomial

If $p\left(x\right)$ is a polynomial in $x$, the highest power of $x$ in $p\left(x\right)$ is called the DEGREE OF THE POLYNOMIAL $p\left(x\right)$.

Linear Polynomial

Let a polynomial $4x+2$.

Variable $x$ of this polynomial has power equal to one (1), thus degree of this polynomial is one (1). Or this is called the Polynomial of degree 1.

A polynomial of degree 1 is known as LINEAR POLYNOMIAL also.

Quadratic Polynomial

Let a polynomial $x^2+x+2$.

Variable $x$ of this polynomial has highest power equal to 2. Thus, this polynomial, variable of which has highest power equal to 2 is called Polynomial of 2 degree.

A polynomial of 2 degree is known as QUADRATIC POLYNOMIAL also.

Cubic Polynomial

A polynomial of degree 3 is called a CUBIC POLYNOMIAL.

Example:

$x^3+2x^2-x+1$, $2-x^3$, $\sqrt{2}x$, etc.

The most general form of a cubic polynomial is

$a{x}^3+b{x}^2+cx+d$ where $a,b,c,d$ are real numbers and $a\ne 0$.

Value of Polynomial

If $p\left(x\right)$ is a polynomial in $x$, and if $k$ is any real number, then the value obtained by preplacing $x$ by $k$ in $p\left(x\right)$, is called the value of $p\left(x\right)$ at $x=k$, and is denoted by $p\left(k\right)$.

Example:

Let a polynomial $p\left(x\right)=x^2-3x-4$

By putting $x=2$, we get

$p\left(2\right)=2^2-3\times 2-4=-6$

Here, the value of $2$ is called the value of polynomial $p\left(x\right)$ at $x=2$.

Zeroes of a Polynomial

A real number $k$ is said to be a zero of a polynomial $p\left(x\right)$, if $p\left(k\right)=0$.

Example:

Let a polynomial $p\left(x\right)=x^2-3x-4$

By putting $x=-1$, we get

$p(-1)={(-1)}^2-3(-1)-4$

$\Rightarrow p(-1)=1+3-4=0$

By putting $x=4$ in the polynomial in example, we get

$p\left(4\right)=4^2-(3\times 4)-4$

$\Rightarrow p\left(4\right)=16-12-4=0$

Since, here $p(-1)=0$ and $p\left(4\right)=0$

Thus, $-1$ and $4$ are called the zeros of the quadratic polynomial $x^2-3x-4$.

Zeroes of a Linear Polynomial

If $k$ is a zero of $p\left(x\right)=ax+b$, then

$p\left(k\right)=ak+b=0$

i.e. $k=\frac{-b}{a}$

Thus, zero of a LINEAR POLYNOMIAL $ax+b$ is equal to $\frac{-b}{a}$

$=\frac{-\text{Constant term}}{\text{Coefficient of}x}$

Thus, zero of a LINEAR POLYNOMIAL is related to its coefficients.

The zeroes of a polynomial $p\left(x\right)$ are precisely the $x-$ coordinates of the points, where the graph of $y=p\left(x\right)$ intersects the $x-$axis.

NCERT Exercise 2.1 Solution Class ten Mathematics

Question: 1. The graphs of $y=p\left(x\right)$ are given in the figure below, for some polynomials $p\left(x\right)$. Find the number of zeros of $p\left(x\right)$, in each case.

(i)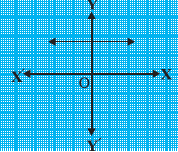 

Answer: Since line of graph does not intersect $x-$axis, thus number of zeros = 0

(ii)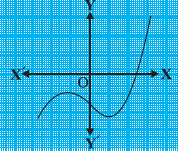 

Answer: Since line of graph  intersects $x-$axis only once, thus number of zeros = 1

(iii)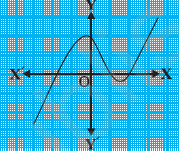 

Answer: Since line of graph intersects $x-$axis thrice, thus number of zeros = 3

(iv)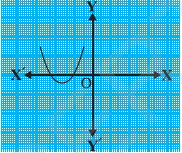 

Answer: Since line of graph intersects $x-$axis twice, thus number of zeros = 2

(v)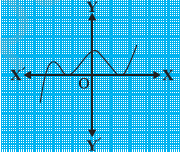 

Answer: Since line of graph intersects $x-$axis three times, thus number of zeros = 3

(vi)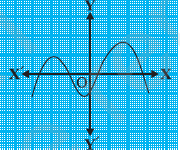 

Answer: Since line of graph intersects $x-$axis four times, thus number of zeros = 4

Relationship between Zeroes and Coefficients of a Polynomial

If $\alpha$ and $\beta$ are the zeroes of the quadratic polynomial $p\left(x\right)=a{x}^2+bx+c$, where$a\ne 0$, then $x-\alpha$ and $x-\beta$ are the factors of $p\left(x\right)$.

Therefore,

$a{x}^2+bx+c$ $=k(x-\alpha )(x-\beta )$, where $k$ is constant.

$=k[x^2(\alpha +\beta )x+\alpha \beta ]$

$=k{x}^2-k(\alpha +\beta )x+k\alpha \beta$

Now, by comparing the coefficients of $x^2,x$ and constant terms on both sides, we get

$a=k$ -------(i)

$b=-k(\alpha +\beta )$ ----------(ii)

$c=k\alpha \beta$ ------(iii)

Now,

∵ $b=-k(\alpha +\beta )$

$\therefore \alpha +\beta =-\frac{b}{k}$

After replacing the value of $k=a$ from equation (i) we get

$\alpha +\beta =-\frac{b}{a}$ -------(iv)

Now,

∵ $c=k\alpha \beta$

$\therefore \alpha \beta =\frac{c}{k}$

After replacing the value of $k=a$ from equation (i) we get

$\alpha \beta =\frac{c}{a}$ ---------(v)

Thus, sum of zeroes

$=\alpha +\beta =-\frac{b}{a}$

$=\frac{-\text{Coefficient of}x}{\text{Coefficient of}{x}^2}$

And Product of zeroes

$=\alpha \beta =\frac{c}{a}=\frac{\text{Constant term}}{\text{Coefficient of}{x}^2}$

NCERT Exercise 2.2 SolutionClass ten Mathematics

Question: 1. Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.

(i) $x^2-2x-8$

Solution:

Given,

$x^2-2x-8$

After expanding middle term $2x$, we get

$=x^2-4x+2x-8$

[∵ $2x=-4x+2x$]

$=x(x-4)+2(x-4)$

Now, after taking $(x-4)$ as common, we get

$=(x-4)(x+2)$

Thus, the value of $x^2-2x-8$ is zero, when $x-4=0$ or $x+2=0$

Thus,

When $x-4=0$

$\therefore x=4$

And, when $x+2=0$

$\therefore x=-2$

Therefore,

The zeroes of $x^2-2x-8$ are 4 and $-2$. Answer

Verification of relationship between zeroes and coefficients.

Now, Sum of zeroes $=4+(-2)=-(-\frac{2}{1})$  $=\frac{-\text{Coefficient of}x}{\text{Coefficient of}{x}^2}$

And Product of zeroes $=4\times (-2)=-\frac{8}{1}$  $=\frac{\text{Constant term}}{\text{Coefficient of}{x}^2}$

(ii) $4s^2-4s+1$

Solution:

Given, $4s^2-4s+1$

$={\left(2s\right)}^2-2\times 2\times s+1$

$={(2s-1)}^2$

[∵ ${(a-b)}^2=a^2-2ab+b^2$]

$=(2s-1)(2s-1)$

Thus, value of $4s^2-4s+1$ is equal to zero (0), when $2s-1=0$

Therefore, when, $2s-1=0$

$\Rightarrow 2s=1$

$\Rightarrow s=\frac{1}{2}$

Thus, the zeroes of $4s^2-4s+1$ are $\frac{1}{2}$ and $\frac{1}{2}$

Verification:

Sum of zeroes $=\frac{1}{2}+\frac{1}{2}=1=-\frac{-4}{4}$

$=\frac{-\text{Coefficient of}s}{\text{Coefficient of}{s}^2}$

Product of zeroes $=\frac{1}{2}\times \frac{1}{2}$

$=\frac{1}{4}=\frac{\text{Constant term}}{\text{Coefficient of}{s}^2}$

(iii) $6x^2-3-7x$

Solution:

Given, $6x^2-3-7x$

$=6x^2-7x-3$

After expanding middle term $-7x$ we get

$=6x^2-9x+2x-3$

[∵ $-9x+2x=-7x$]

$=3x(2x-3)+1(2x-3)$

After taking $2x+3$ as common

$=(2x-3)(3x+1)$

Thus, value of $6x^2-3-7x$ is equal to zero (0), when $2x-3=0$ or $3x+1=0$

Thus, when,

$2x-3=0$

$\therefore 2x=3\Rightarrow x=\frac{3}{2}$

And, when, $3x+1=0$

$\therefore 3x=-1\Rightarrow x=-\frac{1}{3}$

Thus, zeroes of $6x^2-3-7x$ are $\frac{3}{2}$ and $-\frac{1}{3}$

Verification:

Now,

Sum of zeroes $=\frac{3}{2}+(-\frac{1}{3})$

$=\frac{9-7}{6}=\frac{7}{6}$

$=\frac{-(-7)}{6}=\frac{-\text{Coefficient of}x}{\text{Coefficient of}{x}^2}$

And, product of zeroes

$=\frac{3}{2}\times (-\frac{1}{3})=-\frac{3}{6}$

$=\frac{\text{Constant term}}{\text{Coefficient of}{x}^2}$

(iv) $4u^2+8u$

Solution:

Given, $4u^2+8u$

$=4u(u+2)$

Thus, the value of $4u^2+8u$ is zero when, $4u=0$ or $u+2=0$

Thus, when, $4u=0$

$\therefore u=0$

And, when $u+2=0$

$\therefore u=-2$

Therefore, the zeroes of $4u^2+8u$ are $0$ and $-2$

Verification:

Now, Sum of zeroes $=u+(-2)=-2$

$=\frac{-8}{4}=\frac{-\text{Coefficient of}u}{\text{Coefficient of}{u}^2}$

And, product of zeroes $=0\times (-2)=0$

$=\frac{0}{4}=\frac{\text{Constant term}}{\text{Coefficient of}{u}^2}$

(v) $t^2-15$

Solution:

Given, $t^2-15$

$=t^2-{\left(\sqrt{15}\right)}^2$

$=(t+\sqrt{15})(t-\sqrt{15})$

[∵ $a^2-b^2=(a+b)(a-b)$]

Thus, the value of $t^2-15$ is equal to zero, when $t-\sqrt{15}=0$ or $t+\sqrt{15}=0$

Therefore, when $t-\sqrt{15}=0$

$\therefore t=\sqrt{15}$

And when, $t+\sqrt{15}=0$

$\therefore t=-\sqrt{15}$

Thus, zeroes of $t^2-15$ are $\sqrt{15}$ and $-\sqrt{15}$

Verification:

Now, sum of zeroes $=\sqrt{15}+(-\sqrt{15})=0$

$=\frac{-0}{1}=\frac{-\text{Coefficient of}t}{\text{Coefficient of}{t}^2}$

And, product of zeroes $=\sqrt{15}\times (-\sqrt{15})=-15$

$=\frac{-15}{1}=\frac{\text{Constant term}}{\text{Coefficient of}{t}^2}$

(vi) $3x^2-x-4$

Solution:

Given, $3x^2-x-4$

By expanding middle term $-x$, we get

$3x^2+3x-4x-4$

$=3x(x+1)-4(x+1)$

After taking $(x+1)$ as common, we get

$=(x+1)(3x-4)$

Thus, the value of $3x^2-x-4$ is zero when $x+1=0$ or $3x-4=0$

Thus, when, $x+1=0$

Therefore, $x=-1$

And when, $3x-4=0$

Therefore, $3x=4\Rightarrow x=\frac{4}{3}$

Therefore, zeroes of $3x^2-x-4$ are $-1$ and $\frac{4}{3}$

Verification:

Sum of zeroes

$=-1+\frac{4}{3}=\frac{-3+4}{3}=\frac{1}{3}$

$=-\frac{-1}{3}=\frac{-\text{Coefficient of}x}{\text{Coefficient of}{x}^2}$

And, product of zeroes, $=-1\times \frac{3}{4}$

$=\frac{-4}{3}=\frac{\text{Constant term}}{\text{Coefficient of}{x}^2}$

Question: 2. Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.

(i) $\frac{1}{4},-1$

Solution:

Given, Sum and product of zeroes of polynomial are $\frac{1}{4}$ and $-1$ respectively.

Let, the polynomial be $a{x}^2+bx+c$ ------(i)

And its zeroes are $\alpha$ and $\beta$

Thus, according to question,

$\alpha +\beta =\frac{1}{4}=\frac{-b}{a}$

Thus, $a=4$ and $b=-1$

$\alpha \beta =-1=\frac{-4}{4}=\frac{c}{a}$

Therefore, $a=4,b=-1$ and $c=-4$

Thus, after substituting the values of $a,b$ and $c$ in equation (i), we get

$4x^2-1\times x-4$

$=4x^2-x-4$

Therefore, the quadratic polynomial for the given values, is $4x^2-x-4$ Answer

(ii) $\sqrt{2},\frac{1}{3}$

Solution:

Given, the sum and product of the quadratic polynomial are $\sqrt{2}$, and $\frac{1}{3}$

Let, the polynomial be $a{x}^2+bx+c$ ------(i)

And its zeroes are $\alpha$ and $\beta$

Thus, according to question,

Product of zeroes

$=\alpha \beta =\frac{1}{3}=\frac{c}{a}$

Therefore, $c=1$ and $a=3$

Sum of zeroes

$=\alpha +\beta =\sqrt{2}=\frac{-b}{a}$

$\Rightarrow \frac{3\sqrt{2}}{3}=\frac{-b}{a}$

[∵ $a=3$]

Thus, $a=3,b=-3\sqrt{2}$ and $c=1$

After substituting the values of $a,b$ and $c$ in equation (i), we get

$3x^2-3\sqrt{x}+1$

Therefore, the quadratic polynomial for the given values, is $3x^2-3\sqrt{x}+1$ Answer

(iii) $0,\sqrt{5}$

Solution:

Given, the sum and product of the quadratic polynomial are $0$, and $\sqrt{5}$

Let, the polynomial be $a{x}^2+bx+c$ ------(i)

And its zeroes are $\alpha$ and $\beta$

Thus, according to question,

Sum of zeroes

$=\alpha +\beta =0=\frac{0}{1}=\frac{-b}{a}$

And product of zeroes

$=\alpha \beta =\sqrt{5}=\frac{\sqrt{5}}{1}=\frac{c}{a}$

Thus, $a=1,b=-0$ and $c=\sqrt{5}$

After substituting the values of $a,b$ and $c$ in equation (i), we get

$x^2+(-0\times x)+\sqrt{5}$

$=x^2+\sqrt{5}$

Therefore, the quadratic polynomial for the given values, is $=x^2+\sqrt{5}$ Answer

(iv) $1,1$

Solution:

Given, the sum and product of the quadratic polynomial are $1$, and $1$

Let, the polynomial be $a{x}^2+bx+c$ ------(i)

And its zeroes are $\alpha$ and $\beta$

Thus, according to question,

Sum of zeroes

$=\alpha +\beta =1=\frac{1}{1}=\frac{-b}{a}$

And, product of zeroes

$=\alpha \beta =1=\frac{1}{1}=\frac{c}{a}$

Thus, $a=1,b=-1$ and $c=1$

After substituting the values of $a,b$ and $c$ in equation (i), we get

$x^2-x+1$

Therefore, the quadratic polynomial for the given values, is $x^2-x+1$ Answer.

(v) $-\frac{1}{4},\frac{1}{4}$

Solution:

Given, the sum and product of the quadratic polynomial are $-\frac{1}{4}$, and $\frac{1}{4}$

Let, the polynomial be $a{x}^2+bx+c$ ------(i)

And its zeroes are $\alpha$ and $\beta$

Thus, according to question,

Sum of zeroes

$=\alpha +\beta =-\frac{1}{4}=\frac{-b}{a}$

And Product of zeroes,

$=\alpha \beta =\frac{1}{4}=\frac{c}{a}$

Thus, $a=4,b=1$ and $c=1$

After substituting the values of $a,b$ and $c$ in equation (i), we get

$4x^2+x+1$

Therefore, the quadratic polynomial for the given values, is $4x^2+x+1$ Answer.

(vi) $4,1$

Solution:

Given, the sum and product of the quadratic polynomial are $4$, and $1$

Let, the polynomial be $a{x}^2+bx+c$ ------(i)

And its zeroes are $\alpha$ and $\beta$

Thus, according to question,

Sum of zeroes

$=\alpha +\beta =4=\frac{4}{1}=\frac{-b}{a}$

And product of zeroes,

$=\alpha \beta =1=\frac{1}{1}=\frac{c}{a}$

Thus, $a=1,b=-4$ and $c=1$

After substituting the values of $a,b$ and $c$ in equation (i), we get

$x^2-4x+1$

Therefore, the quadratic polynomial for the given values, is $x^2-4x+1$ Answer.