बहुपदNCERT प्रश्नावली 2.1

Welcome to Gurukul with Arya Gautam

बहुपद

Math Class Tenth hindi version एनसीईआरटी  बोर्ड के प्रश्नों के हल

• NCERT प्रश्नावली 2.1

    

बहुपद क्या है? NCERT प्रश्नावली 2.1

चर, अचर, चर के गुणांक तथा ऋणेतर घातांक के जोड़, घटाव या गुणन की क्रिया वाले बीजगणितीय ब्यंजक को बहुपद (POLYNOMIAL) कहा जाता है।

उदारण:

$x^2+4x-7$, $x^3+2x^{2}y-y+1$, $3x$, 5, इत्यादि

दूसरी तरफ $x^{-2}y$, $\frac{1}{x}$, $\frac{2}{x+1}$, $\sqrt{x}$, इत्यादि बहुपद (POLYNOMIAL) नहीं हैं। क्योंकि एक बहुपद (POLYNOMIAL) में निम्नांकित ब्यंजक नहीं हो सकते हैं, या निम्नांकित ब्यंजक वाले बहुपद (POLYNOMIAL) नहीं कहे जाते हैं:

(i) ऋणात्मक चिन्ह वाले घातांक जैसे कि $-2$, $-5$, आदि

(ii) कोई भी पद जो किसी चर से विभाजित हों, यथा $\frac{1}{x}$

(iii) कोई भी भिन्न वाले घातांक जैसे कि $\sqrt{x}$, क्योंकि इसे $x^{\frac{1}{2}}$ तरह लिखा जाता है।

लेकिन एक बहुपद (POLYNOMIAL) में अचर, चर या घात हो सकते हैं।

उदाहरण

अचर (Constants): $3,2,-2,\frac{1}{4}$ etc.

चर (Variables): $x,yx,z,abc$, etc.

घातांक (Exponents): $0,1,2,3,4$, etc.

बहुपद की घात (Degree of Polynomial)

यदि $p\left(x\right)$ एक बहुपद (POLYNOMIAL) है, तो चर $x$, के बहुपद $p\left(x\right)$ में $x$ की उच्चतम घात (Power) बहुपद की घात (Degree of Polynomial) कहलाती है।

रैखिक बहुपद (Linear Polynomial)

मान लिया कि $4x+2$ कि एक बहुपद है।

इस बहुपद के चर $x$ का घात एक (1) है। अत: इस बहुपद को एक घात वाला बहुपद या एक घातीय बहुपद या रैखिक बहुपद कहते हैं।

अत: घात 1 के बहुपद को एक घात वाला बहुपद या रैखिक बहुपद (Linear polynomial) कहते हैं।

द्विघात बहुपद (Quadratic Polynomial)

मान लिया कि $x^2+x+2$ एक बहुपद (Polynomial) है।

इस बहुपद (Polynomial) में चर (Variable) $x$ का उच्चतम घात 2 (दो) है। अत: ऐसे बहुपद को द्विघात बहुपद या द्विघाती बहुपद कहते हैं।

अत: घात 2 (दो) के बहुपद को द्विघात बहुपद (QUADRATIC POLYNOMIAL) कहते हैं।

त्रिघात बहुपद (Cubic Polynomial)

घात 3 (तीन) का बहुपद (Polynomial) त्रिघात बहुपद (CUBIC POLYNOMIAL) कहलाता है।

उदाहरण:

$x^3+2x^2-x+1$, $2-x^3$, $\sqrt{2}x$, इत्यादि

चूँकि इन बहुपदों में चर $x$ की उच्चतम घात 3 (तीन) है, अत: ये सभी त्रिघात बहुपद (Cubic Polynomial) हैं।

त्रिघात बहुपद (Cubic Polynomial) का सबसे व्यापक रूप है:

$a{x}^3+b{x}^2+cx+d$ जहाँ $a,b,c,d$ वास्तविक संख्याएँ हैं और $a\ne 0$ है।

बहुपद का मान (Value of Polynomial)

यदि $p\left(x\right)$, $x$ में कोई बहुपद है और $k$ कोई वास्तविक संख्या है, $p\left(x\right)$ में $x$ को $k$ से प्रतिस्थापित करने पर प्राप्त वास्तविक संख्या $p\left(x\right)$ का $x=k$ पर मान कहलाती है और इसे $p\left(k\right)$ से निरूपित करते हैं।

उदारहण:

मान लिया $p\left(x\right)=x^2-3x-4$

इसमें $x=2$ रखने पर हम पाते हैं कि

$p\left(2\right)=2^{23}\times 2-4=-6$

यहाँ प्राप्त मान $2$, $p\left(x\right)$ का $x=2$ मान कहलाता है।

बहुपद का शून्यक (Zeroes of a Polynomial)

एक वास्तविक संख्या $k$ बहुपद $p\left(x\right)$ का शून्यक (zero of a polynomial) कहलाती है, यदि $p\left(k\right)=0$ है।

उदारण:

मान लिया कि एक बहुपद $p\left(x\right)=x^2-3x-4$

इस बहुपद में $x=-1$ रखने पर हम पाते हैं कि

$p(-1)={(-1)}^2-3(-1)-4$

$\Rightarrow p(-1)=1+3-4=0$

अब इस बहुपद में $x=4$ रखने पर हम पाते हैं कि

$p\left(4\right)=4^2?(3\times 4)-4$

$\Rightarrow p\left(4\right)=16-12-4=0$

चूँकि यहाँ $p(-1)=0$ तथा $p\left(4\right)=0$

अत: $-1$ और $4$ दिये गये बहुपद $x^2-3x-4$ का शून्यक कहलाती है।

रैखिक बहुपद का शून्यक (Zeroes of a Linear Polynomial)

यदि $k$ बहुपद $p\left(x\right)=ax+b$ का शून्यक है, तब

$p\left(k\right)=ak+b=0$

i.e. $k=\frac{-b}{a}$

अत: दिये गये रैखिक बहुपद (LINEAR POLYNOMIAL) $ax+b$ का शून्यक बराबर $\frac{-b}{a}$ है।

व्यापक रूप में, यदि $p\left(x\right)=ax+b$ का एक शून्यक $k$ है, तो $p\left(k\right)=ak+b=0$

अर्थात $k=\frac{-b}{a}$ होगा।

अत: रैखिक बहुपद $ax+b$ का शून्यक

अत: रैखिक बहुपद का शून्यक उसके गुणांकों से संबंधित है। ( Thus, zero of a LINEAR POLYNOMIAL is related to its coefficients.)

बहुपद के शून्यकों का ज्यामितीय अर्थ

व्यापक रूप में, घात $n$ के दिए गए बहुपद $p\left(x\right)$ के लिए, $y=p\left(x\right)$ का ग्राफ $x–$अक्ष को अधिक से अधिक $n$ बिन्दुओं पर प्रतिच्छेद करता है। अत: घात $n$ के किसी बहुपद के अधिक से अधिक $n$ शून्यक हो सकते हैं।

एनoसीoआरoटीo प्रश्नावली 2.1 (NCERT Exercise 2.1)

प्रश्न संख्या: 1. किसी बहुपद $p\left(x\right)$ के लिए, $y=p\left(x\right)$ का ग्राफ नीचे चित्रों में दिया है। प्रत्येक स्थिति में, $p\left(x\right)$ के शून्यकों की संख्या ज्ञात कीजिए।

(i)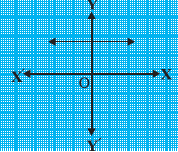 

उत्तर: चूँकि दिये गये ग्राफ में रेखा $x-$axis, को नहीं काटती है, अत: दिये गये बहुपद का कोई शून्यक नहीं है।

अर्थात शून्यक = 0

(ii)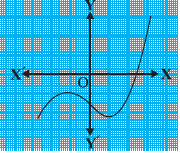 

उत्तर: दिये गये चित्र में दिये गये बहुपद का ग्राफ $x-$अक्ष को केवल एक बार प्रतिच्छेद कर्ता है अर्थात काटता है

अत: दिये गये बहुपद का केवल एक शून्यक है।

 

अत: शून्यक की संख्या = 1

 

(iii)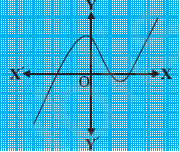 

उत्तर:चूँकि दिये गये चित्र में बहुपद का ग्राफ $x-$अक्ष को तीन बार काटता है।

अत: दिये गये बहुपद के शून्यक की संख्या = 3

(iv)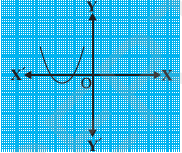 

उत्तर:चूँकि दिये गये चित्र में बहुपद का ग्राफ $x-$अक्ष को दो बार प्रतिच्छेदित करता है, अत: शून्यकों की संख्या = 2 है।

(v)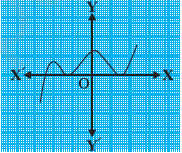 

उत्तर: चूँकि दिये गये चित्र में बहुपद का ग्राफ $x-$अक्ष को तीन बार प्रतिच्छेदित करता है, अत: शून्यकों की संख्या = 3

(vi)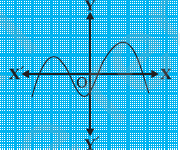 

उत्तर: चूँकि दिये गये चित्र में बहुपद का ग्राफ $x-$अक्ष को चार बार प्रतिच्छेदित करता है, अत: शून्यकों की संख्या = 4

किसी बहुपद के शून्यकों और गुणांकों में संबंध (Relationship between Zeroes and Coefficients of a Polynomial)

यदि $\alpha$ तथा $\beta$ द्विघात बहुपद $p\left(x\right)=a{x}^2+bx+c$, $a\ne 0$ के शून्यक हों, तो $x-\alpha$ और $x-\beta$, $p\left(x\right)$ के गुणनखंड होते हैं।

अत:,

$a{x}^2+bx+c$ $=k(x-\alpha )(x-\beta )$, जहाँ $k$ एक अचर (constant) है।

$=k[x^2(\alpha +\beta )x+\alpha \beta ]$

$=k{x}^2-k(\alpha +\beta )x+k\alpha \beta$

दोनों ओर के $x^2,x$ के गुणांकों तथा अचर पदों की तुलना करने पर, हम पाते हैं कि

$a=k$ -------(i)

$b=-k(\alpha +\beta )$ ----------(ii)

$c=k\alpha \beta$ ------(iii)

अब,

∵ $b=-k(\alpha +\beta )$

$\therefore \alpha +\beta =-\frac{b}{k}$

उक्त में समीकरण (i) से $k=a$ प्रतिस्थापित करने पर हम पाते हैं कि

$\alpha +\beta =-\frac{b}{a}$ -------(iv)

अब,

∵ $c=k\alpha \beta$

$\therefore \alpha +\beta =\frac{c}{k}$

उक्त में समीकरण (i) से $k=a$ प्रतिस्थापित करने पर हम पाते हैं कि

$\alpha +\beta =\frac{c}{a}$ ---------(v)

अत: शून्यकों का योग (sum of zeroes)

$=\alpha +\beta =$

तथा शून्यकों का गुणनफल (Product of zeroes)

$=\alpha \beta =\frac{c}{a}$ =