Light: Reflection & Refraction - Class 10th Science
Introduction
Light travels in straight line. An opaque object obstructs rays of light when it comes in the path of light, and casts a shadow, this phenomenon tells that rays of light travels in straight line.
When rays of light fall on an object, they bounce back and come to our eyes. Bouncing back of light after falling on an object to our eyes enables us to see a particular object. We cannot see an object in dark, because there is no light present in dark which can be bounced back to our eyes.
Reflection of Light
Bouncing back of rays of light from an object is called REFLECTION OF LIGHT.
A highly polished surface reflects most of the light falling on it. For example a mirror, which has polished surface, reflects most of the light falling on it.
Incident Ray
Rays of light which falls on a reflecting surface is called Incident Ray.
Reflected Ray
Rays of light bouncing back from a reflecting surface is called Reflected Ray.
Normal
An imaginary line perpendicular to reflecting surface at the point of falling of ray of light is called NORMAL or normal to the Reflecting surface.
Angle of Incidence
Angle at which ray of light falls on a reflection surface to the normal is called ANGLE OF INCIDENCE.
Angle of Reflection
Angle at which ray of light bounces back from a reflecting surface to the normal is called ANGLE OF REFLECTION.
Laws of Reflection
(i) The angle of reflection of incidence is equal to the angle of reflection, and
(ii) The incident ray, the normal to the mirror, at the point of incidence and their reflected ray, all lie in the same plane.
Laws of Reflection are applied to all type of reflecting surfaces.
Types of Reflecting Surface
Reflecting surfaces may be plane, curved, spherical or uneven.
Spherical Mirrors
Spherical mirrors are of two types. One which reflecting surface is curved inwards and other with reflecting surface outwards.
Spherical mirrors having reflecting surface curved inwards are called CONCAVE MIRROR or CONCAVE SHPERICAL MIRROR.
Spherical mirrors having reflecting surface curved outwards are called CONVEX MIRROR or CONVEX SPHERICAL MIRROR.
Example: A spoon having reflecting surface inwards is similar to a concave mirror and having reflecting surface outwards is similar to a convex mirror.
Reflecting surface of a spherical mirror forms a part of sphere.
Important terms for Spherical Mirror
Pole
The centre of reflecting surface of a spherical mirror is called pole. Pole is denoted by letter 'P'.
Centre of Curvature
Since spherical mirror is a part of a sphere, thus centre of the sphere is called the centre of curvature of the spherical mirror.
Centre of curvature is not the part of spherical mirror and it lies outside of its reflecting surface.
The centre of curvature lies in front of a Concave mirror while centre of curvature lies behind the mirror.
Centre of curvature is conventionally denoted by letter 'C'.
Radius of Curvature
The radius of sphere of which spherical mirror is a part is called the Radius of Curvature of the spherical mirror.
Radius of curvature is also not the part of reflecting surface of the spherical mirror. Similar to Centre of Curvature, Radius of Curvature also lies outside of the spherical mirror.
In the case of concave mirror radius of curvature lies in front of spherical surface while in the case of convex mirror it lies behind the reflecting surface.
Radius of Curvature is denoted by letter 'R'.
Principal Axis
An imaginary line passes through the pole and centre of curvature of a spherical mirror is called PRINCIPAL AXIS.
The Principal Axis of a spherical mirror is normal to the mirror at its pole.
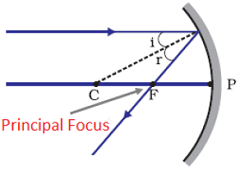
Focus
Rays coming from infinity are parallel to the principal axis and pass through a point of spherical mirror. This point is called FOCUS or PRINCIPAL FOCUS of a spherical mirror. Focus is known as Focal Point also.
Focus of a concave mirror lies in front of reflecting surface while in the case of convex mirror Focus lies behind the reflecting surface.
Focus or Principal Focus is denoted by letter 'F'.
Focal Length
The distance from Focus to Pole of a spherical mirror is called Focal Length. Focal length is denoted by letter 'f'.
Focal length is half of the radius of curvature.
Therefore, R = 2f
This means focal length of a spherical mirror lies midway between the pole and the centre of curvature.
Aperture
The diameter of the reflecting surface of a spherical mirror is called its APERTURE.
Spherical mirror can be of many sizes. Spherical mirror having big size has large aperture while spherical mirror having small size has small aperture.
Reflection of light through Spherical Mirror
Reflection of Ray of light coming from infinity from Concave Mirror
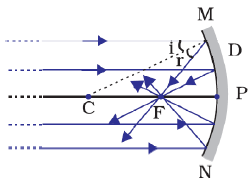
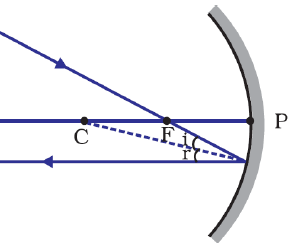
Rays of light coming from infinity travels parallel to principal axis. After reflecting through surface of concave mirror, it passes through principal focus of the mirror.
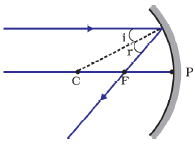
All rays of light coming through infinity travels parallel to principal axis and pass through principal focus after reflecting from concave mirror.
Here angle of incidence 'i' is equal to the angle of reflection 'r'. In this case DC is normal to the point of reflection.
Since, a Convex Mirror converge all rays coming from infinity to its principal focus, thus a Convex Mirror is known as Converging Mirror also.
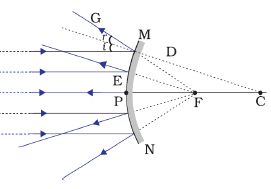
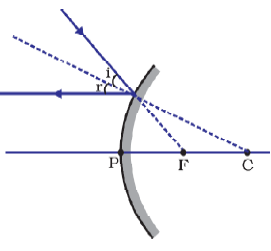
Reflection of Ray of light coming from infinity from Convex Mirror
Ray of light coming from infinity travels parallel to principal axis and appears to passing through principal focus after reflection from a Convex Mirror.
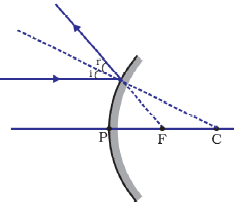
All rays coming from infinity travel parallel to principal axis and appear passing through the principal focus after reflecting from a convex mirror.
Since, all rays coming from infinity diverge after reflection from a Concave mirror, thus a Concave Mirror is known as Diverging Mirror also.
Reflection of ray of light directing through the Principal Focus from a Concave Mirror
A ray of light directing through the principal focus of a concave mirror passes towards parallel to the principal axis after reflection from a concave mirror.
This is just opposite to the ray directing parallel to the principal axis.
Reflection of ray of light directing through the Principal Focus from a Convex Mirror
A ray of light directing through the principal Focus passes parallel to the principal axis after reflection from a Convex Mirror.
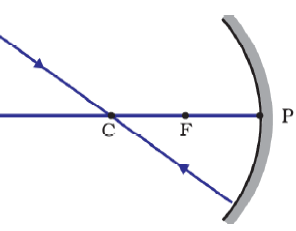
Reflection of ray passing through the centre of curvature of the Concave Mirror
Ray of light passing or directing through the centre of curvature redirects on the same path, i.e. from the centre of curvature in the same direction after reflection from a Concave Mirror.
Reflection of ray passing through the centre of curvature of the Convex Mirror
Ray of light passing or directing through the centre of curvature redirects on the same path, i.e. from the centre of curvature in the same direction after reflection from a Convex Mirror.
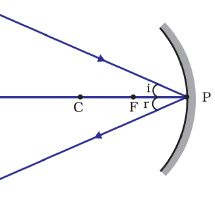
Reflection of ray of light incident obliquely to the Principal axis towards a Pole of a Concave Mirror
A ray of light incident obliquely to the Principal axis towards pole, directs obliquely to the principal axis after reflection from a Concave Mirror at the same angle of incident.
Reflection of ray of light incident obliquely to the Principal axis towards a Pole of a Convex Mirror
A ray of light incident obliquely to the Principal axis towards pole, directs obliquely to the principal axis after reflection from a Convex Mirror at the same angle of incident.
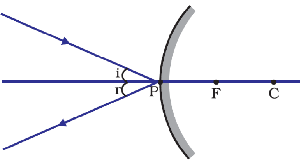
Since, reflection of light from any surface follows the Laws of Reflection, thus in all the cases, angle of incidence (i) to the normal is equal to the angle of reflection (r) to the normal.
Real Image: Image which can be cast on screen is called Real Image. Real image is formed always in front of mirror.
Virtual Image: Image which cannot be cast on screen is called Virtual or Imaginary Image. Virtual image is formed behind the mirror.
Image Formation by Concave Mirror
To find the position of image formation by a mirror, at least two rays are taken into consideration. One ray is generally taken which directs parallel to principal axis and second ray which passes through centre of curvature. The meeting point of these rays is considered as the position of image.
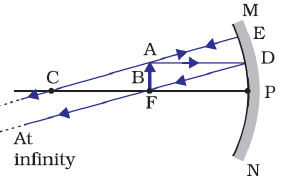
(a) When object at infinity in the case of Concave Mirror
Rays coming from object at infinity are parallel to principal axis, and converge at Principal Focus of Concave Mirror after reflection.
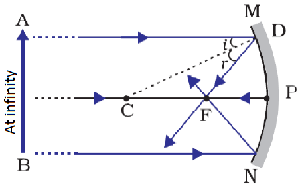
Position of Image: Since rays converges at Principal focus, thus image is formed at Focus, F
Size of Image: Highly diminished and point size.
Nature of Image: Real and Inverted
(b) When object is beyond Centre of Curvature (C)
When object is placed beyond the centre of curvature, rays from object pass through principal focus as image formed between principal focus and centre of curvature.
Position of image: Between Principal Focus (F) and Centre of Curvature (C)
Size of Image: Diminished
Nature of Image: Real and Inverted
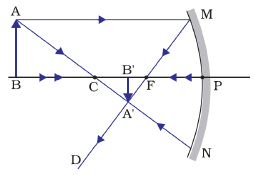
(c) When object is at centre of curvature (C)
When object is placed at the centre of curvature, image formed at the same place, i.e. at the centre of curvature (C), but just opposite to it.
Position of image: At Centre of Curvature (C)
Size of Image: Same size
Nature of Image: Real and Inverted
(d) When object is between Centre of Curvature (C) and Principal Focus (F)
When object is placed between Centre of Curvature (C) and Principal Focus (F) of a concave mirror, in this case image is formed beyond Centre of Curvature (C).
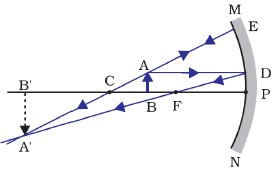
Position of image: Beyond Centre of Curvature (C)
Size of Image: Enlarge
Nature of Image: Real and Inverted
(e) When object is at Principal Focus (F)
When object is placed at Principal Focus (F) of a concave mirror, image is formed at infinity.
This is just opposite of the position of object at infinity. Image formed at principal focus (F) when object is placed at infinity, just opposite of it image formed at infinity when object is placed at principal focus (F) by a concave mirror.
Position of image: At infinity
Size of Image: Highly Enlarge
Nature of Image: Real and Inverted
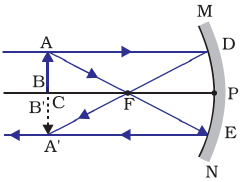
(f) Image formation by a Concave Mirror when object is placed between Pole (P) and Principal Focus (F)
When object is placed between pole (P) and principal focus (F), image is formed behind the mirror by a concave mirror.
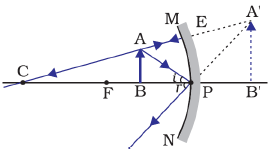
Position of image: Behind the mirror
Size of Image: Enlarge
Nature of Image: Virtual and Erect
| Image Formation by a Concave Mirror | |||
|---|---|---|---|
| Position of Object | Position of Image | Size of Image | Nature of Image |
| At infinity | At Focus (F) | Highly diminished (Point sized) | Real and Inverted |
| Beyond C | Between F & C | Diminished | Real and Inverted |
| At C | At C | Same size | Real and Inverted |
| Between C and F | Beyond C | Enlarged | Real and Inverted |
| At F | At infinity | Highly Enlarged | Real and Inverted |
| Between P and F | Behind the mirror | Enlarged | Virtual and Erect |
Use of Concave Mirror
Concave mirror is used in torches, search lights and vehicles head lights. In these lights, bulb is kept at the principal focus of concave mirror. This gives parallel beams of light.
Concave mirror is used in shaving mirrors to see a larger image of face.
Concave mirror is used by dentists to see the larger image of teeth of patient.
Large Concave mirrors are used in solar furnace to concentrate the sunlight to get heat. Large concave mirror has large aperture, due to which it reflects more sun light and concentrate at focus which give large amount of heat.
Image Formation by Convex Mirror
Since, Principal focus (F) and Centre of Curvature (C) lie behind a convex mirror. Therefore, only two positions arise to place object infront of a Convex Mirror.
These positions are
(a) Object at infinity, and
(b) Object between pole (P) and infinity
(a) Image formation by a Convex Mirror when object is at Infinity
When object is placed at infinity, rays coming parallel to principal axis appear to converge at principal focus (F) after reflection from a concave mirror. Thus, image formed at principal focus (F) by a concave mirror.
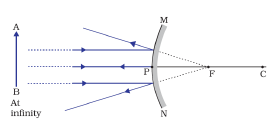
Position of image: At principal Focus (F)
Size of Image: Highly diminished (Point sized)
Nature of Image: Virtual and erect
(b) Image formation by a Convex Mirror when object is between pole (P) and infinity
When object is between pole and infinity, image is formed between pole (P) and principal focus (F) by a convex mirror. Image so formed by a convex mirror is virtual, erect and diminished.
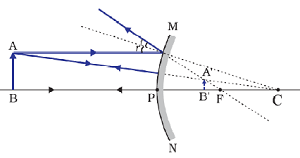
Position of image: Between pole (P) and principal focus (F)
Size of Image: Diminished
Nature of Image: Virtual and erect
Use of Convex Mirror
Convex mirror is used as rear view mirror in vehicles. Convex mirror fitted at the sides of vehicles enable driver to see traffic behind. By watching and judging traffic behind a driver can drive safely. Concave mirror is perfect as rear view mirror in vehicles as it gives an erect image. Concave mirror has wider field of view also. So, a concave mirror is preferred to a plane mirror as rear view mirror.
Concave mirror is used at steep curved path, to see the vehicles or anything coming from other side.
Sign Convention of Reflection by Spherical Mirror
Set of sign convention of reflection by spherical mirror is called New Cartesian Sign Convention also.
Rules of New Cartesian Sign Convention
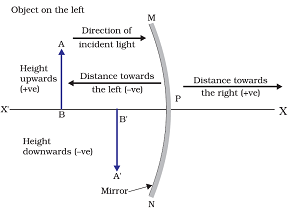
The pole (P) of the mirror is taken as origin. The principal axis of the mirror is taken as the x–axis of the coordinate system. The conventions are as follows:
(i) The object is always placed to the left of the mirror. This implies that the light from the object falls on the mirror from the left hand side.
(ii) All distances parallel to the principal axis are measured from the pole of the mirror.
(iii) All the distances measured to the right of the origin (along + x–axis) are taken as positive while those measured to the left of the origin (along – x–axis) are taken as negative.
(iv) Distances measured perpendicular to and above the principal axis (along + y–axis) are taken as positive.
(v) Distances measured perpendicular to and below the principal axis (along – y–axis) are taken as negative.
Mirror Formula and Magnification
There is relationship among distance of object (u), distance of image (v) and focal length (f) for a mirror, which is expressed as
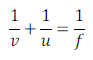
Where, u = distance of object from pole of mirror
v = distance of image from pole of mirror
f = focal length (distance between principal focus and pole)
Expression for the relationship among distance of object (u), distance of image (v) and focal length (f) for a mirror is called mirror formula.
This mirror formula is valid in all situations for all spherical mirrors for all positions of the object.
By knowing any two quantities, third can be calculated using mirror formula.
Magnification
Magnification produced by a spherical mirror gives the relative extent to which the image of an object is magnified with respect to the object size.
Magnification is expressed as the ratio of height of the image to the height of the object. Magnification is conventionally expressed by letter 'm'.
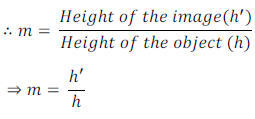
Magnification is related to the distance of object (u) and distance of image (v) also. The ratio of distance of image and distance of object gives magnification too.
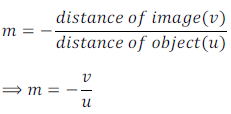
Thus, by knowing the distance of object and image produced by a spherical mirror, magnification can be calculated.
Refraction of Light
Phenomenon of bending of ray of light towards normal while entering from rarer medium to denser medium and vice versa is called the Refraction of Light.
When light enters from rare medium, say air to a denser medium say water, it bends towards normal and when enters from denser medium to rarer medium, say from water to air, it goes away from normal. This phenomenon is called The Refraction of Light.
Example:
When a pencil is put in a glass full of water, pencil appears bent. This happens because of refraction of light.
When a coin is kept in a tub filled with water, it appears slightly above the bottom.
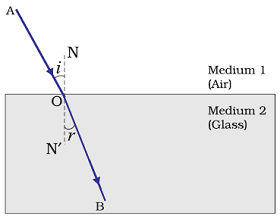
Laws of Refraction of Light
(i) The incident ray, the refracted ray and the normal to the interface of two transparent media at the point of incidence, all lie in the same plane.
(ii) The ratio of sine of the angle of incidence to the sine of angle of refraction is a constant, for the light of a given colour and for the given pair of media.
This law is known as Snell's Law of Refraction of Laws of Refraction of light.
If angle of incidence is 'i' and angle of refraction is 'r', then according to the Laws of Refraction of Light
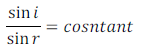
The constant value is called the Refractive Index of the second medium with reference to the first.
Refractive Index
Refractive Index is the extent of change in direction of light while travelling from one medium to another medium.
In other words, ratio of the angle of sine of incidence to the angle of sine refraction for the given pair of media is called the Refractive Index.
Refractive Index and speed of Light
Value of Refractive index is related to the relative speed of light in different media. Light travels with different speed in different media. The speed of light is 3 x 108 m s– in vacuum which is fastest and slightly less than in air.
Speed of light decreases with denser media.
Refractive Index of Light in one medium with respect to other
Let light enters from medium 1 to medium 2.
Let, v1 is the speed of light in medium 1
Let, v2 is the speed of light in medium 2
∴ The refractive index of medium 2 with respect to medium 1 is given by the ratio of the speed of light in medium 1 and the speed of light in medium 2.
This is generally represented by the symbol n2 1
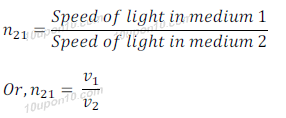
Refractive Index of medium 1 with respect to medium 2
Let light enters from medium 2 to medium 1.
Let, v1 is the speed of light in medium 1
Let, v2 is the speed of light in medium 2
∴ The refractive index of medium 1 with respect to medium 2 is given by the ratio of the speed of light in medium 2 and the speed of light in medium 1.
This is generally represented by the symbol n1 2
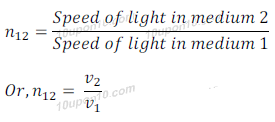
Refractive Index when one of the medium is vacuum
The value of Refractive index of a medium with respect of vacuum is called ABSOLUTE REFRACTIVE INDEX.
In other words, Absolute Refractive Index is the refractive index of a medium with respect of vacuum.
Example, let if medium 1 is vacuum and medium 2 is any other medium
Therefore,
Absolute Refractive Index of the given medium (nm)

The absolute refractive index of a medium is simply called its Refractive Index.
For example Refractive index of air (na) is 1.0003, Refractive Index of Ice (ni) is 1.31, Refractive index of Water (nw) is 1.33, etc.
Optical Density
The ability of a medium to refract light is also expressed in terms of its OPTICAL DENSITY. Optical density is not the same as mass density.
Denser medium means Optically denser medium and Rarer medium means Optically rarer medium.
Optically Denser Medium:
Medium which has greater or larger Refractive Index is called optically denser medium.
Optically Rarer Medium:
Medium which has lesser or smaller Refractive Index is called optically rarer medium. For Example: Refractive Index of Kerosene oil is 1.44 and Refractive Index of ice is 1.31. Therefore in the comparison of Ice and kerosene oil, Ice is optically rarer medium while kerosene oil is optically denser medium.
Speed of Light in different Medium:
Speed of light is fastest in vacuum. Speed of light decreases with increase in refractive index and increases with decrease in refractive index. This means speed of light is greater in rarer medium while lesser in denser medium.
Example: Refractive Index of crown glass is 1.52 while of Fused quartz is 1.46. This means crown glass is denser medium than fused quartz. Thus, speed of light is greater in fused quartz than that of crown glass.
Since speed of light decreases in denser medium, because of this when light enter from a rarer medium to denser medium, it bends towards normal and when light enters from denser medium to rarer medium light bends away from normal.
Thus, it is the speed of light in different medium which causes Refraction of Light.
Lens
A transparent material bound by two surfaces of which one or both surfaces are spherical, is called lens.
Types of Lens:
Convex Lens
A lens having two spherical surface bulging outwards is called Convex Lens. A convex lens is called double convex lens also.
A convex lens is thicker at the middle as compared to the edges.
A convex lens converges rays of light pass through it, so a convex lens is known as CONVERGING LENS also.
Concave Lens
A lens having two spherical surface curved inwards is called Concave Lens. A concave lens is thicker at edges than at the middle.
A concave lens diverges rays of light, hence a concave lens is called DIVERGING LENS also.
Important terms of Spherical Lens
Centre of Curvature: A spherical lens is formed by the parts of the combination of two spherical surfaces. The centres of these spheres are called the centre of curvature of the lens.
There are two centre of curvature of a lens on either side.
Generally centre of curvature of a lens is represented by C1 and C2 respectively.
Optical Centre: The central point of a lens is called its optical centre. The optical centre of a lens is generally denoted by letter 'O'.
Principal axis: An imaginary line passing through the centre of curvatures of al lens is called Principal Axis.
Principal Focus: Point at which rays coming parallel to the principal axis converge is called the Principal Focus of a convex lens.
In the case of Concave lens, point at which rays coming parallel to the principal axis appear to be diverged is called Principal Focus of a Concave lens.
There are two principal focus, which lie either side of a spherical lens. These principal focus are generally represented by F1 and F2.
Focal Length: Distance between Principal focus (F) and optical centre (O) of a spherical lens is called Focal Length of a spherical lens. Focal length is represented by letter 'f'.
Focal length is equal to half of the centre of curvature, i.e. C1 = 2F1
Refraction by a Spherical Lens
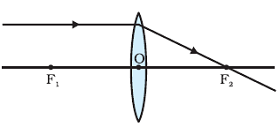
Refraction of Rays coming parallel to principal axis to convex lens
Rays coming parallel to the principal axis are passes through the principal focus after refraction from a convex lens.
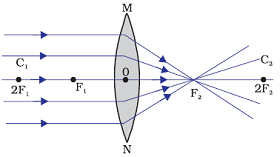
Refraction of Rays coming parallel to principal axis to concave lens
Rays coming parallel to the principal axis are appeared to passes through the principal focus after refraction from a concave lens.
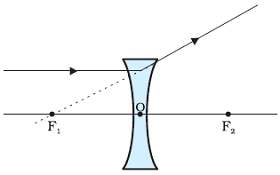
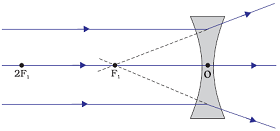
Refraction of Ray of light passing through the principal focus from a convex lens
A ray of light passing through the principal focus emerges parallel to the principal axis after refraction from a convex lens.
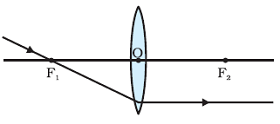
Refraction of Ray of light passing through the principal focus from a concave lens
A ray of light appearing to meet at the principal focus of a concave lens will emerge parallel to the principal axis after refraction.
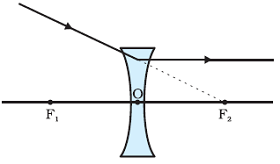
Refraction of Ray passing through the optical centre of a spherical lens
A ray of light passing through the optical centre of a lens will emerge without any deviation after refraction from a spherical lens.
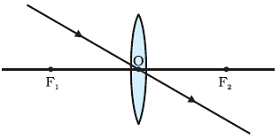
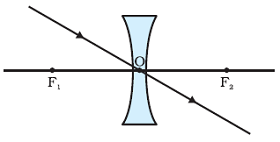
Image Formation by Convex Lens
Image formation by a convex lens when object is at infinity
When object is at infinity, image is formed by a convex lens is at principal focus.
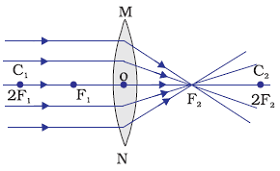
Position of image: At focus F2
Relative size of the image: Highly diminished, point sized
Nature of the image: Real and inverted
Image formation by a convex lens when object is beyond centre of curvature (C1)
When object is beyond centre of curvature (C1), i.e. beyond 2F1 of a convex lens, image is formed between principal focus (F2) and centre of curvature (C2 or 2F2).
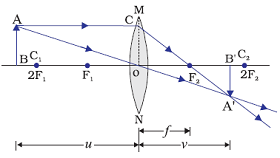
Position of image: between principal focus (F2) and centre of curvature (C2 or 2F2)
Relative size of the image: Diminished
Nature of the image: Real and inverted
Image formation by a convex lens when object is at centre of curvature (C1 or 2F1)
When object is at 2F1, i.e. at centre of curvature (C1), image is formed at other side of centre of curvature (C2), i.e. at 2F2 by a convex lens.
Position of image: At 2F2 i.e. at centre of curvature (C2)
Relative size of the image: Same size
Nature of the image: Real and inverted
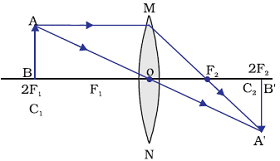
Image formation by a convex lens when object between F1 and 2F1
When object is placed between F1 and 2F1, an enlarge image is formed beyond 2F2 by a convex lens.
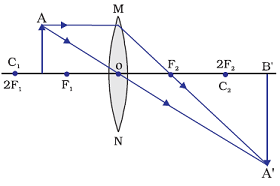
Position of image: Beyond 2F2 i.e. beyond centre of curvature (C2)
Relative size of the image: Enlarged
Nature of the image: Real and inverted
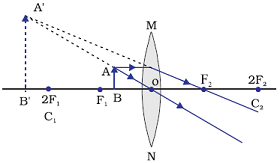
Image formation by a convex lens when object is at Focus (F1)
When image is placed at focus (F1), a highly enlarge image is formed at infinity by a convex lens.
Position of image: At infinity
Relative size of the image: Highly Enlarged
Nature of the image: Real and inverted
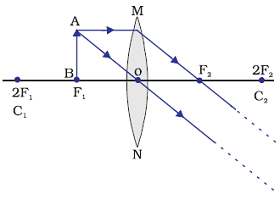
Image formation by a convex lens when object between focus (F1) and optical centre (O)
When object is placed between focus (F1) and optical centre (O), an enlarge image is formed at same side beyond 2F1 by a convex lens.
Position of image: At same side beyond 2F1
Relative size of the image: Enlarged
Nature of the image: Virtual and Erect
Image Formation by Concave Lens
Similar to a convex mirror only two conditions arise to place an object infront of a concave mirror for image formation. These positions are
First object is at infinity and second object is between infinity and optical centre (O).
Image formation by a concave lens when object is at infinity
When object is placed at infinity, a diminished imaged is formed by a concave lens at focus (F1).
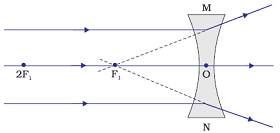
Position of image: At focus (F1)
Relative size of the image: Highly diminished, point sized
Nature of the image: Virtual and Erect
Image formation by a concave lens when object is between infinity and optical center (O)
When object is placed between infinity and optical centre (O), a diminished image is formed between focus (F1) and optical centre by a concave lens.
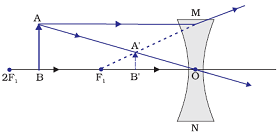
Position of image: Between focus (F1) and optical centre (O)
Relative size of the image: Diminished
Nature of the image: Virtual and Erect
Sign convention for Spherical Lenses
Sign conventions for spherical lens are similar to spherical mirror.
Set of sign convention of reflection by spherical mirror is called New Cartesian Sign Convention also.
Rules of New Cartesian Sign Convention
The pole (P) of the mirror is taken as origin. The principal axis of the lens is taken as the x–axis of the coordinate system. The conventions are as follows:
(i) The object is always placed to the left of the lens. This implies that the light from the object falls on the lens from the left hand side.
(ii) All distances parallel to the principal axis are measured from the pole of the lens.
(iii) All the distances measured to the right of the origin (along + x–axis) are taken as positive while those measured to the left of the origin (along – x–axis) are taken as negative.
(iv) Distances measured perpendicular to and above the principal axis (along + y–axis) are taken as positive.
(v) Distances measured perpendicular to and below the principal axis (along – y–axis) are taken as negative.
Lens Formula and Magnification
Lens formula gives the relationship between distance of object (u), distance of image (v) and focal length (f).
Lens formula tells that reciprocal of focal length is equal to the reciprocal of distance of image minus reciprocal of distance of object. This can be expressed as follows:
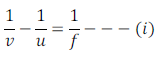
Expression (i) is known as the lens formula. This lens formula is valid in all situations for any spherical lens.
Magnification
The magnification produced by a spherical lens is given by the ratio of height of image to the height of object. Magnification is generally denoted by letter 'm'.
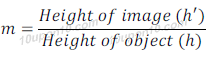
Magnification (m) produced by a spherical lens is related to distance of image and distance of object too.
Thus,
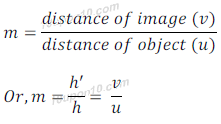
Power of Lens
The ability to converge or diverge rays of light depends on the focal length of a spherical lens. The ability of converge or diverge rays of light is indirectly proportional to the focal length.
This means a lens with greater focal length has less converging or diverging ability of rays of light.
Example: A convex lens of short focal length bends the light rays through large angles by focusing them closer to the optical centre. Similarly, a concave lens of very short focal length causes higher divergence than one with longer focal length.
The degree of convergence or divergence of light rays achieved by a lens is expressed in terms of its power.
Since, ability to convergence or divergence of a lens depends on the focal length of a lens, and ability to convergence of divergence is called the power of lens. Thus, power of a lens is related to the focal length of a lens.
The power of a lens is denoted by letter 'P'.
The power of a lens is the reciprocal of its focal length.
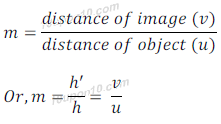
The SI unit of power of a lens is 'dioptre' and is denoted by letter 'D'.
If focal length (f) of a lens is denoted in meter (m), then power of the lens is denoted by dioptres.
1 dipotre is the power of a lens whose focal length is 1 meter.
Thus, 1D = 1m–
Negative and Positive Power of a lens
Power of a Convex lens is expressed with positive sign (+) and power of a Concave lens is expressed with negative (–) sign.
Example: If a doctor prescribed a spectacle with power of glass equal to +1 dioptre, this means the lens is convex.
And if the power of prescribed lens of spectacle is equal to –2 dipotre, this means the lens is concave.
The net Power
Optical instruments, such as a high quality telescope, consist of number of lenses. Many lenses are combined to increase the magnification and sharpness of image.
If there are four lenses having power of P1, P2, P3, and P4 are in contact in an optical instrument,
Then net power of lens (P) = P1 + P2 + P3 + P4
How power of lens is prescribed by an optician
While testing the eye, if an optician found, the two lenses with power of 2.00 D and 0.25 D is suitable for a patient with eye problem.
Then, net power (P) of the lens = 2.00 D + 0.25 D = 2.25 D
Thus, optician prescribes a power of 2.25 D to the patient.
In Text Solution
Question: 1. Define the principal focus of a concave mirror.
Answer: Rays coming from infinity are parallel to the principal axis pass through a point of spherical mirror. This point is called FOCUS or PRINCIPAL FOCUS of a spherical mirror. Focus is known as Focal Point also.
Focus of a concave mirror lies in front of reflecting surface while in the case of convex mirror Focus lies behind the reflecting surface.
Focus or Principal Focus is denoted by letter 'F'.
Question: 2. The radius of curvature of a spherical mirror is 20 cm. What is its focal length.
Answer: Radius of curvature = 2 x Focal length
Here given, Radius of curvature = 20 cm
Therefore, Focal length = 20 cm / 2
Or, Focal length = 10 cm Answer
Question: 3. Name the mirror that can give and erect and enlarged image of an object.
Answer: Concave mirror
Explanation: A concave mirror produces an erect and enlarged image behind the mirror when object is placed between F (Focus) and P (Pole).

Question: 4. Why we prefer a convex mirror as a rear view mirror in vehicles?
Answer: A concave mirror is preferred as a rear view mirror in vehicles because
A convex mirror gives an erect and smaller image.
A convex mirror has wider field of view as it is curved outwards which enable a driver to view much larger area than would be possible with a plane mirror.
A convex mirror enables the driver to see traffic behind him because of features given above and facilitate safe driving.
Question: 5. Find the focal length of a convex mirror whose radius of curvature is 32 cm.
Answer: Given, Radius of curvature = 32 cm
We know that Focal length = Radius of curvature / 2
Therefore, Focal length = 32 cm / 2 = 16 cm Answer
Question: 6. A concave mirror produces three times magnified (enlarged) real image of an object placed at 10 cm in from of it. Where is the image located?
Answer: Given,
Distance of object (u) = – 10 cm (Since, object is infront of mirror, thus a minus sign is added before the distance of object)
Magnification (m) = 3
Distance of image (v) = ?
We know that

Here, minus sign before the distance of image shows that image is formed infront of mirror and image is real.
Thus location of image is 30 cm in front of concave mirror.
Question: 7. A ray of light travelling in air enters obliquely into water. Does the light ray bend towards the normal or away from the normal? Why?
Answer: When ray of light travelling in air enter obliquely into water, it bends towards the normal.
When ray of light enters from optically rarer medium to denser medium, it bends towards normal and vice versa. This is called refraction of light. This happens because light travels at higher speed in optically rarer medium and its speed decreases when enters in a optically denser medium.
Here, water is optically denser medium than that of water. Since, speed of light is greater in air than water, thus when light enters in water from air, it bends towards normal.
Question: 8. Light enters from air to glass having refractive index 1.50. What is the speed of light in the glass? The speed of light in vacuum is 3 x 10 8 m s –1.
Answer: Given,
Speed of light in vacuum (c) = 3 x 10 8 m s –1
Since, speed of light in air is almost similar to that of vacuum,
Thus, speed of light in air = 3 x 10 8 m s –1
Refractive Index of glass (ng = 1.50
Speed of light in the given glass (v) = ?
We known that,

Question: 9. Find out, from Table 10.3, the medium having highest optical density. Also find the medium with lowest optical density.
Answer: As given in table 10.3
Refractive Index of air = 1.0003
And Refractive Index of diamond = 2.42
Refractive Index is reciprocal of optical density. This means refractive index increases with decrease in optical density and vice versa. Medium which has lower optical density is rarer medium and that having higher optical density is denser medium.
Since, diamond has highest Refractive Index and air has lowest Refractive Index
Thus, Diamond has lowest optical density and air has highest optical density.
Question: 10. You are given kerosene, turpentine and water. In which of these does the light travel fastest? Use the information given Table 10.3.
Answer: According to Table 10.3
Refractive Index of Kerosene = 1.44
Refractive Index of turpentine = 1.47
Refractive Index of water = 1.33
Medium which has higher Refractive Index is optically denser medium. And light travels with lower speed in optically denser medium and vice versa.
Here Refractive Index of the water is lowest, i.e. 1.33 compare to kerosene and turpentine.
Thus, light travels with fastest speed in water among given medium, i.e. kerosene, turpentine and water.
Question: 11. The refractive index of diamond is 2.42. What is the meaning of this statement?
Answer: Refractive Index of a medium tells that how much denser or rarer a medium is. Medium having higher Refractive Index is optically denser medium.
Here, given the refractive index of diamond is 2.42, this statement tells that diamond is optically highly denser medium.
Question: 12. Define 1 dioptre of power of a lens.
Answer: If focal length is expressed in meters, then power is expressed in diopters.
Thus, 1 diopter of power of a lens whose focal length is 1 meter
Or, 1D = 1m –1
Question: 13. A convex lens forms a real and inverted image of a needle at a distance of 50cm from it. Where is the needle placed in front of the convex lens. If the image is equal to the size of the object? Also, find the power of the lens.
Answer: When object is placed at the 2F1 of a convex lens, an equal size image is formed at the other side, i.e. at 2F2 of the convex lens.
Here, given
Distance of image = 50cm
Therefore, distance of object = – 50cm
Thus, needle is placed at 2F1 in front of the convex lens.
We know that, focal length of a convex lens = 2F1 /2
Here, Radius of curvature = 2F1 = 50cm = 0.5m
Or, Focal length (f) = 0.50 m / 2 = 0.25m
We know that power of a lens (P) = 1/f
Or, P = 1/0.25m
Or, P = + 4 dioptre
Hence, needle is placed at 2F1 in front of the convex lens, i.e. 50cm in front of convex lens.
And power of lens = + 4 dioptre
Question: 14. Find the power of a concave lens of focal length 2m.
Answer: Given, focal length (f) = 2m
We know that power of a lens (P) = 1/f
Or, P = 1/2m = 0.5 dioptre
Since, lens is concave, thus power will be in minus.
Thus, power of given lens = – 0.5 dioptre
NCERT Exercise Solution
Question: 1. Which one of the following materials cannot be used to make a lens?
(a) Water
(b) Glass
(c) Plastic
(d) Clay
Answer: (d) Clay
Explanation: Clay is an opaque material while water, glass and plastic are transparent. Thus, clay cannot be used to make a lens.
Question: 2. The image formed by a concave mirror is observed to be virtual, erect and larger than the object. Where should be the position of the object?
(a) Between the principal focus and the centre of the curvature
(b) At the centre of curvature
(c) Beyond the centre of curvature
(d) Between the pole of the mirror and its principal focus
Answer: (d) Between the pole of the mirror and its principal focus
Explanation: A virtual and erect image is formed only when object is placed only between the pole of the mirror and its principal focus.

Apart from this by placing object at all other possible positions, a real image is formed by a concave mirror.
Question: 3. Where should an object be placed in front of a convex lens to get a real image of the size of the object?
(a) At the principal focus of the lens
(b) At twice the focal length
(c) At infinity
(d) Between the optical centre of the lens and its principal focus
Answer: (b) At twice the focal length
Explanation: When object is placed at 2F1, i.e. at twice of the focal length, an inverted, equal sized and real image is formed at 2F1 by a convex lens.

Question: 4. A spherical mirror and a thin spherical lens have each a focal length of –15 cm. The mirror and the lens are likely to be
(a) Both concave
(b) Both convex
(c) the mirror is concave and the lens is convex
(d) the mirror is convex, but the lens is concave
Answer: (a) Both concave
Explanation: Distance of a concave mirror and concave lens is measured with negative sign according to sign convention.
Here, since, focal length is given with negative sign, thus, given lens and mirror is concave.
Question: 5. No matter how far you stand from a mirror, your image appears erect. The mirror is likely to be
(a) Plane
(b) Concave
(c) Convex
(d) either plane or convex
Answer: (d) either plane or convex
Explanation: A plane mirror and a convex mirror always forms and erect image intead of the distance of object from the mirror.
Thus, option (d) either plane or convex is the correct answer.
Question: 6. Which of the following lenses would you prefer to use while reading small letters found in a dictionary?
(a) A convex lens of focal length 50cm.
(b) A concave lens of focal length 50cm.
(c) A convex lens of focal length 5cm
(d) A concave lens of focal length 5cm
Answer: (c) A convex lens of focal length 5cm
Explanation: When object is placed between F1 and optical centre, a real, enlarged and erected image is formed beyond 2F2 by a convex lens.
Thus, it is convenient to use a convex lens of focal length of 5cm while reading small letters found in a dictionary. Convex lens with this focal length will produce image at a convenient distance to read.
If a convex lens having focal length of 50cm is used, then image formed by it will be at a distance of more than 1meter, to read at such distance will not be convenient.
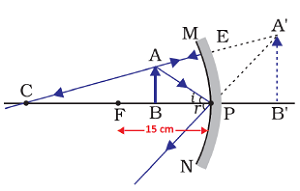
Question: 7. We wish to obtain an erect image of an object, using a concave mirror of focal length 15cm. What should be the range of distance of the object from the mirror? What is the nature of the image? Is the image larger or smaller than the object? Draw a ray diagram to show the image formation in this case.
Answer: A concave mirror forms a virtual, enlarged and erect image only when object is placed between its principal focus and pole.
Thus, in given situation of a concave lens having focal length equal to 15cm, the object must be placed less than 15cm from pole of the mirror to get an erect image.
Thus, range of distance of the object from the mirror = less than 15cm
Nature of image: Virtual and erect
Size of image: Larger than the object
Question: 8. Name the type of mirror used in the following situations.
(a) Headlights of a car
(b) Side/rear view mirror of a vehicle
(c) Solar furnace
Support your answer with reason.
Answer:
(a) Headlights of a car: Concave mirror is used.
Explanation: When object is placed at principal focus of a concave mirror, rays coming from object direct parallel to the principal axis and a highly enlarged, real and inverted image is formed at infinity.
Thus, in headlights of a car, by placing bulb (source of light) at principal focus of a concave mirror, a parallel beam of light is obtained which goes up to infinity. This facilitates better vision upto a long distance to the driver.
(b) Side/rear view mirror of a vehicle: A convex mirror is used.
Explanation: A concave mirror is used as side/rear view mirror of a vehicle because:
A convex mirror gives an erect and smaller image.
A convex mirror has wider field of view as it is curved outwards which enable a driver to view much larger area than would be possible with a plane mirror.
A convex mirror enables the driver to see traffic behind him because of features given above and facilitate safe driving.
(c) Solar furnace: A concave mirror is used having large aperture.
Explanation: A concave mirror converges light rays coming parallel to its principal axis from infinity at its principal focus.
By converging rays of light at a point, all heat of light get focused at one point and produce enormous heat.
Thus, in a solar furnace, a concave mirror having large size of aperture is used.
NCERT Exercise Solution: Q:9-16
Question: 9. One half of a convex lens is covered with a black paper. Will this lens produce a complete image of the object? Verify your answer experimentally. Explain your observations.
Answer: Yes, if one half of a convex lens is covered with a black paper, it produces a complete image of the object.
Experiment:
One half of a convex lens covered with black paper is taken.
An object is placed infront of it, say beyond 2F1
It produces a diminished, real and inverted image between F2 and 2F2
Experiment is repeated by placing object at different positions.
In all cases image is formed.
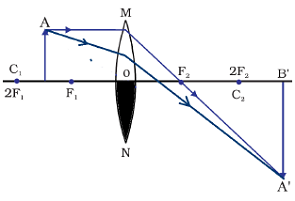
Since, rays coming from object passes through the upper part and optical centre of the lens, so a half portion covered convex lens with black paper produces image easily.
Question: 10. An object 5cm in length is held 25cm away from a converging lens of focal length 10cm. Draw the ray diagram and find the position, size and the nature of the image formed.
Answer: Here given,
Size of object: 5cm
Distance of object (u): –25cm
Focal length (f) = 10cm
Distance of image (v) =?
We know that in the case of a converging lens 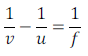
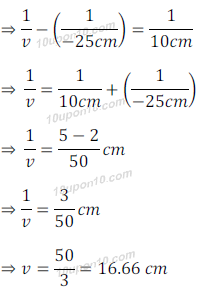
We know that, magnification

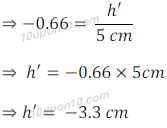
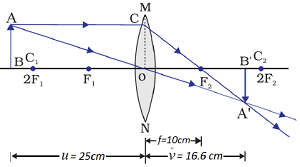
Position of image: Between F2 and 2F2, i.e. at the other side of lens.
Size of image: – 3.3 cm, i.e. smaller than object.
Nature of image: Inverted and real
Question: 11. A concave lens of focal length 15cm forms an image 10cm from the lens. How far is the object placed from lens? Draw a ray diagram.
Answer: Given,
Focal length of concave lens (f) = – 15cm
Distance of image (v) = – 10cm
Distance of object (u) = ?
We know that in the case of a converging lens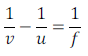
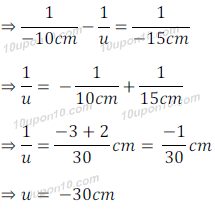
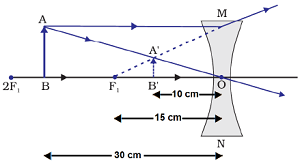
Thus, object is place at distance of 30cm from the lens i.e. at 2F1 of the concave lens.
Question: 12. An object is placed at a distance of 10cm from a convex mirror of focal length 15cm. Find the position and nature of the image.
Answer: Given,
Distance of object (u) = – 10cm
Focal length = 15cm
Therefore, Distance of image (v) =?
We know that for a spherical mirror 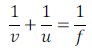
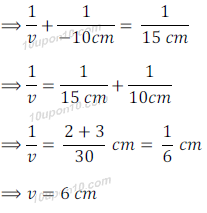
Now, magnification

Since distance of image is positive, this shows that image is formed at the other side of the mirror. And magnification is also positive this shows that image is erect.
Thus, Position of image = 6cm (behind the mirror, because distance of image is positive)
Nature of image = Virtual and erect (Because magnification is positive and image is formed behind the mirror)
Question: 13. The magnification produced by a plane mirror is +1. What does it mean?
Answer: Magnification produced by a plane mirror is +1 means,
(a) Size of image is equal to the size of object
(b) Positive sign in the magnification shows that image is erect.
Explanation: A plane mirror always form image of same size as of the size of object. And a plane mirror always forms a virtual and erected image.
Question: 14. An object 5.0 cm in length is placed at a distance of 20cm in front of a convex mirror of radius of curvature 30cm. Find the position of the image, its nature and size.
Answer: Given
Size of objet = 5.0 cm
Distance of object = – 20cm
Radius of curvature (R) = 30cm
Thus, focal length = R/2 = 30cm/2 = 15cm
Distance of image (v) = ?
And magnification (m) = ?
We know that, 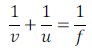
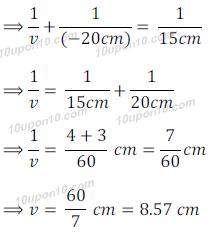

Thus,
Position of image = 8.57 cm behind the mirror
Size of image = 2.15 cm which is smaller than the object
Nature of image = virtual and erect (Because distance of image and magnification both are positive)
Question: 15. An object of size 7.0 cm is placed at 27cm in front of a concave mirror of focal length 18cm. At what distance from the mirror should a screen be placed, so that a sharp focused image can be obtained? Find the size and the nature of the image.
Answer:
Size of object (h) = 7.0 cm
Distance of object (u) = – 27cm
Focal length (f) = – 18cm
Distance of image (v) =?
Height of image (h') =?
We know that, 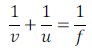
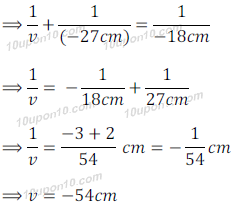

Thus,
To obtain a sharp and focused image, screen will be placed at a distance of 54cm in front of mirror.
Position of image = 54 cm in front of mirror.
Size of image = 14 cm, i.e. double size of object, i.e. enlarged.
Nature of image = Inverted and real (Because magnification and distance of image are in negative)
Question: 16. Find the focal length of a lens of power – 2.0 D. What type of lens is this?
Answer: Given,
Power of lens (P) = – 2.0 D
Thus, focal length (f) =?
We know that, P = 1/f
Or, – 2.0 D = 1/f
Or, f = 1/– 2.0 D
Or, Focal length (f) = – 0.5 m
Since, power of length is in minus, thus it is a concave lens.
Question: 17. A doctor has prescribed the corrective lens of power + 1.5 D. Find the focal length of the lens. Is the prescribed lens diverging or converging?
Answer: Given,
Power of lens (P) = + 1.5 D
Thus, focal length (f) =?
We know that, P = 1/f
∴ + 1.5 D = 1/f
Or, f = 1/1.5D =0.66 m
Thus, focal length of the lens is equal to 0.66 m.
And lens is converging because power given has positive sign.











