प्रश्नावली 6.1 class9th

Welcome to Gurukul with Arya Gautam

 

एनसीईआरटी प्रश्नावली 6.1

नवम गणित (Mathematics Nine:Hindi Medium)

रेखाएँ और कोण: क्लास नौवीं गणित

•   

एनसीईआरटी प्रश्नावली 6.1

रेखाएँ और कोण क्लास नौवीं गणित एनसीईआरटी प्रश्नावली 6.1 प्रश्न संख्या (1) आकृति में, रेखाएँ AB और CD बिन्दु O पर प्रतिच्छेद करती हैं। यदि ∠AOC + ∠BOE = 70o है और ∠BOD = 40o है, तो ∠BOE और प्रतिवर्ती ∠COE ज्ञात कीजिए।

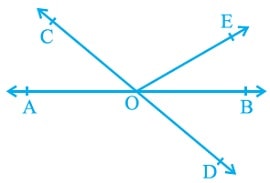
रेखाएँ और कोण क्लास नौवीं गणित एनसीईआरटी प्रश्नावली 6.1 प्रश्न संख्या (1) का हल

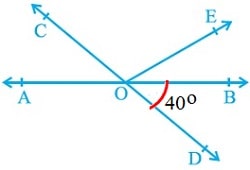
दिया गया है, ∠BOD = 40o

तथा ∠AOC + ∠BOE = 70o

अत: ∠BOE = ?

तथा, ∠COE = ?

जैसा कि प्रश्न में दिया गया है, ∠AOC + ∠BOE = 70o

⇒ ∠BOD + ∠BOE = 70o

[चूँकि ∠BOD तथा ∠AOC शीर्षाभिमुख कोण हैं अत: आपस में बराबर हैं]

⇒ 40o + ∠BOE = 70o

⇒ ∠BOE = 70o – 40o

⇒ ∠BOE = 30o - - - - (i)

अब ∠EOD + ∠COE = 180o

[चूँकि ∠EOD तथा ∠COE कोणों का रैखिक युग्म बनाते हैं अत: संपूरक हैं।]

⇒ ∠BOE + ∠BOD + ∠COE = 180o

⇒ 30o + 40o + ∠COE = 180o

[चूँकि समीकरण (i) के अनुसार ∠BOE = 30o तथा प्रश्न के अनुसार ∠BOD = 40o है।]

⇒ 70 + ∠COE = 180o

⇒ ∠COE = 180o – 70o

⇒ ∠COE = 110o

अत: ∠BOE = 30o तथा ∠COE = 110o उत्तर

रेखाएँ और कोण क्लास नौवीं गणित एनसीईआरटी प्रश्नावली 6.1 प्रश्न संख्या (2) आकृति में, रेखाएँ XY तथा MN बिन्दु O पर प्रतिच्छेद करती हैं। यदि ∠POY = 90o और a : b = 2 : 3 है, तो c ज्ञात कीजिए।

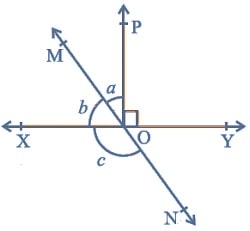
रेखाएँ और कोण क्लास नौवीं गणित एनसीईआरटी प्रश्नावली 6.1 प्रश्न संख्या (2) का हल

दिया गया है, ∠POY = 90o

तथा a : b = 2 : 3

अत: c = ?

∠POY + ∠XOP = 180o

[चूँकि ∠POY तथा ∠XOP कोणों का एक रैखिक युग्म बनाते हैं।]

⇒ 90o +∠XOP = 180o

⇒ ∠XOP = 180o – 90o

⇒ ∠XOP = 90o

अब, जैसा कि प्रश्न में दिया गया है, a : b = 2 : 3

मान लिया कि a = 2x तथा b = 3x

अब, a + b = ∠XOP

⇒ a + b = 90o

⇒ 2x + 3x = 90o

⇒ 5x = 90o

$\therefore x=\frac{{90}^o}{5}$

⇒ x = 18o

अब, चूँकि a = 2x

अत: x = 18o रखने पर हम पाते हैं कि

a = 2 × 18o

⇒ a = 36o

तथा, b = 3x

अत: x = 18o रखने पर हम पाते हैं कि

b = 3 × 18o

⇒ b = 54o - - - - - (i)

अब, ∠XOM + ∠XON = 180o

[चूँकि ∠XOM तथा ∠XON कोणों का रैखिक युग्म बनाते हैं।]

⇒ b + c = 180o

[चूँकि कोण XOM = b तथा कोण XON = c]

⇒ 54o + c = 180o

[चूँकि कोण b = 54o समीकरण (i) के अनुसार]

⇒ c = 180o – 54o

⇒ c = 126o उत्तर

रेखाएँ और कोण क्लास नौवीं गणित एनसीईआरटी प्रश्नावली 6.1 प्रश्न संख्या (3) आकृति में यदि∠PQR = ∠PRQ है, तो सिद्ध कीजिए कि ∠PQS = ∠PRT है।

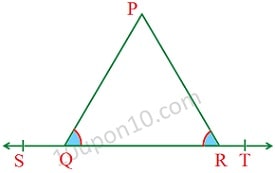
रेखाएँ और कोण क्लास नौवीं गणित एनसीईआरटी प्रश्नावली 6.1 प्रश्न संख्या (3) का हल

दिया गया है, ∠PQR = ∠PRQ

अत: सिद्ध करना है कि ∠PQS = ∠PRT.

प्रमाण

∠PQR + ∠PQS = 180o - - - - - (i)

[चूँकि ∠PQR तथा ∠PQS कोणों का रैखिक युग्म बनाते हैं।]

तथा, ∠PRQ + ∠PRT = 180o - - - - - (ii)

[चूँकि ∠PRQ तथा ∠PRT कोणों का रैखिक युग्म बनाते हैं।]

अब समीकरण (i) तथा समीकरण (ii) से

∠PQR + ∠PQS = ∠PRQ + ∠PRT

अब, जैसा कि प्रश्न में दिया गया है ∠PQR = ∠PRQ अत: उपरोक्त ब्यंजक में ∠PQR के स्थान पर ∠PRQ रखने पर हम पाते हैं कि

∠PRQ + ∠PQS = ∠PRQ + ∠PRT

⇒ ∠PRQ + ∠PQS – ∠PRQ = ∠PRT

⇒ ∠PQS = ∠PRT प्रमाणित

रेखाएँ और कोण क्लास नौवीं गणित एनसीईआरटी प्रश्नावली 6.1 प्रश्न संख्या (4) आकृति में, यदि x + y = w + z, तो सिद्ध कीजिए कि AOB एक रेखा है।

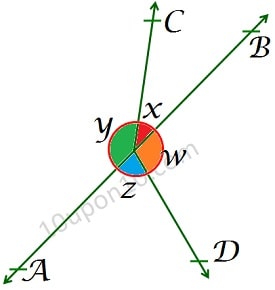
रेखाएँ और कोण क्लास नौवीं गणित एनसीईआरटी प्रश्नावली 6.1 प्रश्न संख्या (4) का हल

दिया गया है, x + y = w + z

तो सिद्ध करना है कि: AOB एक रेखा है।

प्रमाण :

∠x + ∠y + ∠w + ∠z = 360o

[चूँकि किसी बिन्दु के चारों ओर के कोणों का योग = 360o होता है।]

⇒ (∠x + ∠y) + (∠w + ∠z) = 360o

⇒ (∠x + ∠y) + (∠x + ∠y) = 360o

[चूँकि जैसा कि प्रश्न में दिया गया है x + y = w + z]

⇒ 2(∠x + ∠y) = 360o

$\therefore \Rightarrow \angle x+\angle y=\frac{{360}^o}{2}$

⇒ ∠x + ∠y = 180o

⇒ ∠w + ∠z = 180o

[चूँकि जैसा कि प्रश्न में दिया गया है x + y = w + z]

अत: रैखिक युग्म अभिगृहीत के अनुसार जो कहता है कि यदि दो संगत कोणों का योग 180o हो तो कोणों की भुजाएँ जो उभयनिष्ठ नहीं हैं एक सरल रेखा होती है।

अत: AOB एक रेखा है चूँकि ∠x + ∠y = 180o तथा ∠w + ∠z = 180o. प्रमाणितरेखाएँ और कोण क्लास नौवीं गणित एनसीईआरटी प्रश्नावली 6.1 प्रश्न संख्या (5) आकृति में, POQ एक रेखा है। किरण OR रेखा PQ पर लम्ब है। किरणों OP तथा OR के बीच में OS एक अन्य किरण है। तो सिद्ध कीजिए कि

∠ROS = 1/2 (∠QOS – ∠POS

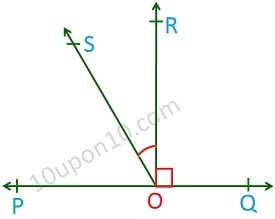
रेखाएँ और कोण क्लास नौवीं गणित एनसीईआरटी प्रश्नावली 6.1 प्रश्न संख्या (5) का हल

दिया गया है, किरण OR रेखा PQ पर लम्ब है। तथा OS एक अन्य रेखा है जो किरणों OP तथा OR के बीच में है।

अत: सिद्ध करना है कि ∠ROS = 1/2 (∠QOS – ∠POS

प्रमाण

चूँक़ि किरण OR रेखा PQ पर लम्ब है

अत: ∠POR = 90o

⇒ ∠POS + ∠SOR = 90o - - - - - (i)

[चूँकि ∠POR = ∠POS + ∠SOR]

तथा, ∠POS + ∠QOS = 180o

[चूँकि ∠POS तथा ∠QOS कोणों का रैखिक युग्म बनाते हैं]

⇒ ∠POS + ∠QOS = 2(∠POS + ∠SOR)

[चूँकि समीकरण (i) से ∠POS + ∠SOR = 90o, अत: 2(∠POS + ∠SOR) = 180o]

⇒ ∠POS + ∠QOS = 2 ∠POS + 2 ∠SOR

∠POS को दायाँ पक्ष में ले जाने पर

⇒ ∠QOS = 2 ∠POS + 2 ∠SOR – ∠POS

⇒ ∠QOS = 2 ∠POS – ∠POS + 2 ∠SOR

⇒ ∠QOS = ∠POS + 2 ∠SOR

⇒ ∠QOS – ∠POS = 2 ∠SOR

⇒ 2 ∠SOR = ∠QOS – ∠POS

⇒ ∠SOR = 1/2(∠QOS – ∠POS) प्रमाणित

रेखाएँ और कोण क्लास नौवीं गणित एनसीईआरटी प्रश्नावली 6.1 प्रश्न संख्या (6) यह दिया गया है कि ∠XYZ = 64o है और XY को बिन्दु P तक बढ़ाया गया है। दी हुयी सूचना से एक आकृति खींचिए। यदि किरण YQ, ∠ZYP को समद्विभाजित करती है, तो ∠XYQ और प्रतिवर्ती ∠QYP के मान ज्ञात कीजिए।

रेखाएँ और कोण क्लास नौवीं गणित एनसीईआरटी प्रश्नावली 6.1 प्रश्न संख्या (6) का हल

दिया गया है, ∠XYZ = 64o

तथा, XY को बिन्दु P तक बढ़ाया गया है।

तथा, किरण YQ, ∠ZYP को समद्विभाजित करती है।

अत: दी हुयी सूचना से निम्नांकित आकृति खींची जा सकती है।

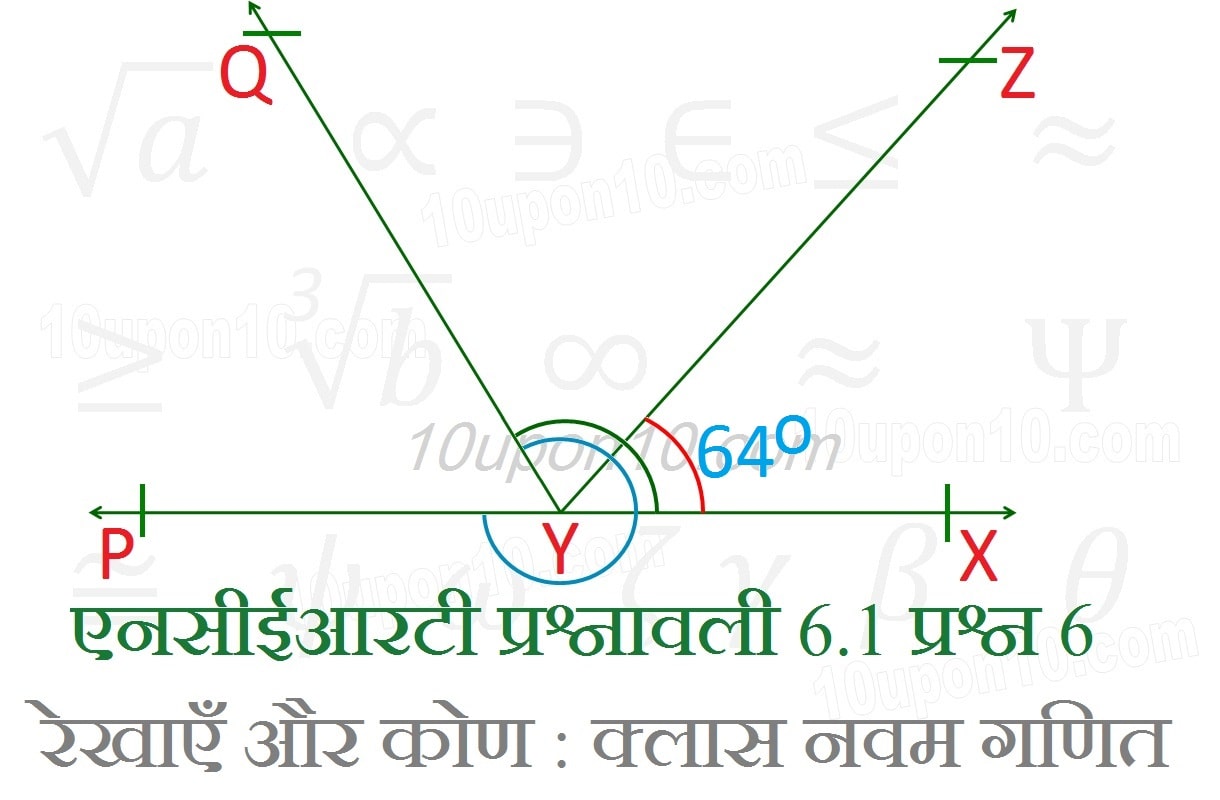
अत: ∠XYQ तथा प्रतिवर्ती ∠QYP = ?

अब, चूँकि PX एक सरल रेखा है।

अत: ∠ZYP + ∠XYZ = 180o

⇒ ∠ZYP + 64o = 180o

⇒ ∠ZYP = 180o – 64o

⇒ ∠ZYP = 116o

अब, जैसा कि प्रश्न में दिया गया है QY, ∠ZYP को समद्विभाजित करती है।

अत: ∠ZYQ = 1/2 ∠ZYP

⇒ ∠ZYQ = 1/2 × 116o

⇒ ∠ZYQ = 58o

अब, ∠XYQ = ∠XYZ + ∠ZYQ

⇒ ∠XYQ = 64o + 58o

⇒ ∠XYQ = 122o

अब, प्रतिवर्ती ∠QYP = ∠XYQ + ∠XYP

⇒ ∠QYP = 122o + 180o

[चूँकि ∠XYP एक सरल रेखा है जिसके कोण की माप 180o होती है।]

⇒ ∠QYP = 302o

अत: ∠XYQ = 122o तथा प्रतिवर्ती कोण ∠QYP = 302o