Welcome to Gurukul with Arya Gautam

Class 10 Maths Solutions Chapter 9 त्रिकोणमिति के कुछ अनुप्रयोग Ex 9.1

📘 कक्षा 10 गणित

✨ अध्याय – त्रिकोणमिति का अनुप्रयोग (Applications of Trigonometry)

---

🌟 परिचय

त्रिकोणमिति = त्रिकोण का मापन
👉 इस अध्याय में हम सीखते हैं कि ऊँचाई (Height) और दूरी (Distance) कैसे निकाली जाती है बिना सीधे नापे।

---

🔑 मुख्य बातें

🔹 1. दृश्य कोण (Angle of Elevation)
➡ जब कोई व्यक्ति ज़मीन पर खड़ा होकर ऊपर देखे।
📍 क्षैतिज रेखा और दृष्टि रेखा के बीच का कोण।

🔹 2. अवनी कोण (Angle of Depression)
➡ जब कोई व्यक्ति ऊँचाई पर खड़ा होकर नीचे देखे।
📍 क्षैतिज रेखा और दृष्टि रेखा के बीच का कोण।

🔹 3. त्रिकोणमितीय अनुपात

$$\sin \theta = \frac{P}{H}, \quad \cos \theta = \frac{B}{H}, \quad \tan \theta = \frac{P}{B}$$

(P = लम्ब, B = आधार, H = कर्ण)

---

🛠 अनुप्रयोग (Applications)

✅ इमारत, मीनार, पेड़ की ऊँचाई निकालना
✅ नदी या सड़क की चौड़ाई निकालना
✅ जहाज़, नाव, पतंग, विमान की दूरी या ऊँचाई मापना
✅ पहाड़ और घाटियों का मापन

---

📌 उदाहरण

👉 किसी इमारत की चोटी का दृश्य कोण 30° है और इमारत से दूरी 50 m है।

$$\tan 30^\circ = \frac{ऊँचाई}{50}$$ $$\frac{1}{\sqrt{3}} = \frac{ऊँचाई}{50}$$ $$ऊँचाई = \frac{50}{\sqrt{3}} \; \text{मीटर}$$

---

📝 निष्कर्ष

🌿 त्रिकोणमिति का अनुप्रयोग हमें बताता है कि केवल कोण और दूरी से हम ऊँचाई और गहराई जैसी कठिन चीज़ों को भी आसानी से निकाल सकते हैं।
👉 पूरा अध्याय समकोण त्रिभुज (Right-angled Triangle) पर आधारित है।

---

✨ "त्रिकोणमिति का अनुप्रयोग हमें यह सिखाता है कि सिर्फ कोण और दूरी से ही ऊँचाई और गहराई का राज़ खोला जा सकता है।
👉 अगर नोट्स अच्छे लगे तो इसे Share करो, Follow करो और सीखते रहो!" ✨

---

 Board Exam Class 10 Maths Solutions Chapter 9 त्रिकोणमिति के कुछ अनुप्रयोग Ex 9.1

प्रश्न 1. सर्कस का एक कलाकार एक 20 m लम्बी डोर पर चढ़ रहा है जो अच्छी तरह से तनी हुई है और भूमि पर सीधे लगे खम्भे के शिखर से बँधी हुई है। यदि भूमि स्तर के साथ डोर द्वारा बनाया गया कोण 30° का हो, तो खम्भे की ऊँचाई ज्ञात कीजिए।

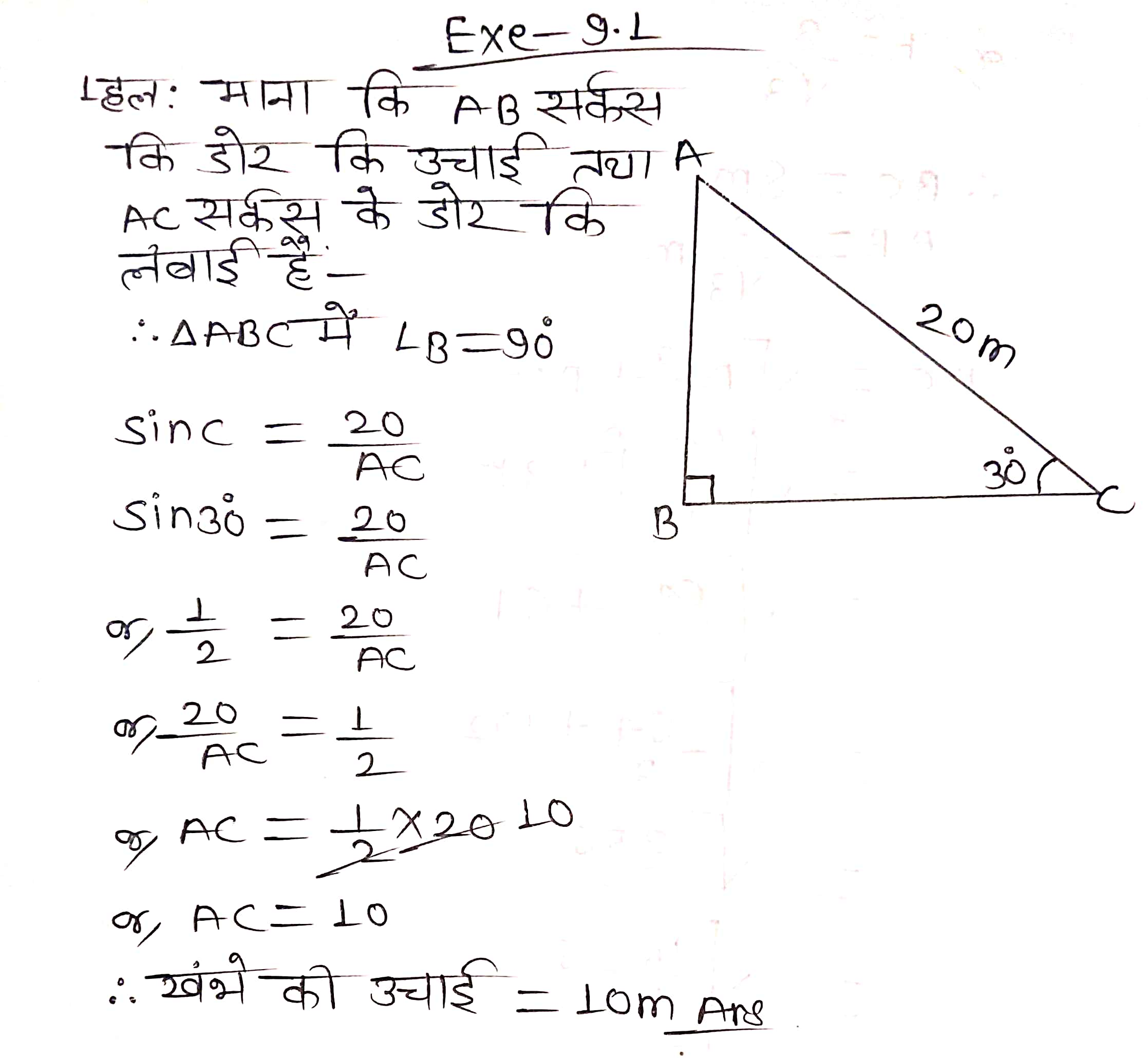
प्रश्न 2. आँधी आने से एक पेड़ टूट जाता है और टूटा हुआ भाग इस तरह मुड़ जाता है कि पेड़ का शिखर जमीन को छूने लगता है और इसके साथ 30° का कोण बनाता है। पेड़ के पाद-बिन्दु की दूरी, जहाँ पेड़ का शिखर जमीन को छूता है, 8 m है। पेड़ की ऊँचाई ज्ञात कीजिए।

 

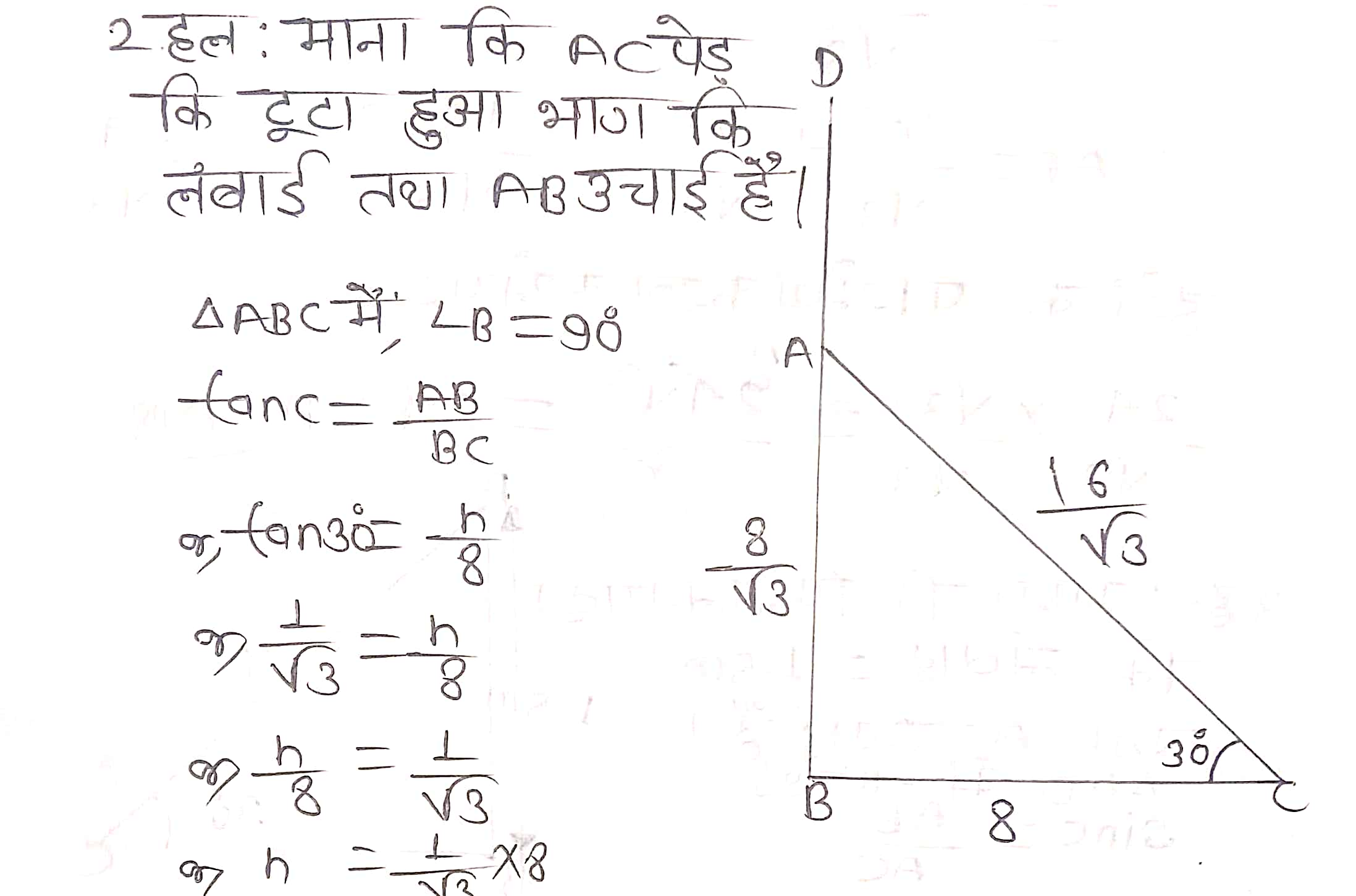
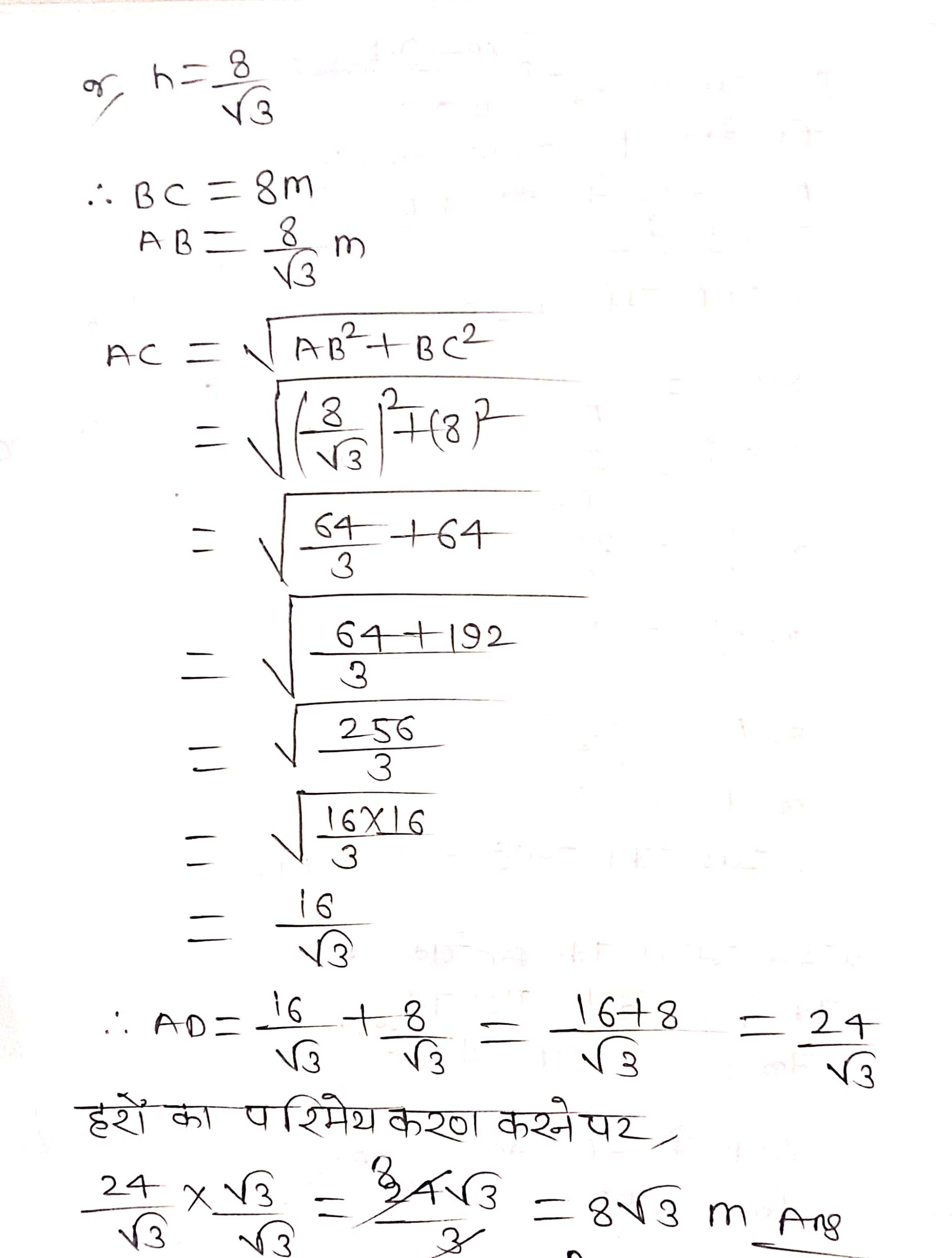
प्रश्न 3. एक ठेकेदार बच्चों को खेलने के लिए एक पार्क में दो फिसलनपट्टी लगाना चाहती है। 5 वर्ष से कम उम्र के बच्चों के लिए वह एक ऐसी फिसलनपट्टी लगाना चाहती है जिसका शिखर 1.5 m की ऊँचाई पर हो और भूमि के साथ 30° के कोण पर झुका हुआ हो, जबकि इससे अधिक उम्र के बच्चों के लिए वह 3 m की ऊँचाई पर एक अधिक ढाल की फिसलनपट्टी लगाना चाहती है, जो भूमि के साथ 60° का कोण बनाती हो। प्रत्येक स्थिति में फिसलनपट्टी की लम्बाई क्या होनी चाहिए?

 

प्रश्न 4. भूमि के एक बिन्दु से जो मीनार के पाद-बिन्दु से 30 m की दूरी पर है, मीनार के शिखर का उन्नयन कोण 30° है। मीनार की ऊँचाई ज्ञात कीजिए। (√3 = 1.73)

प्रश्न 5. भूमि से 60 m की ऊँचाई पर एक पतंग उड़ रही है। पतंग में लगी डोरी को अस्थायी रूप से भूमि के एक बिन्दु से बाँध दिया गया और भूमि के साथ डोरी का झकाव 60° है। यह मानकर कि डोरी में कोई ढील नहीं है, डोरी की लम्बाई ज्ञात कीजिए।

 

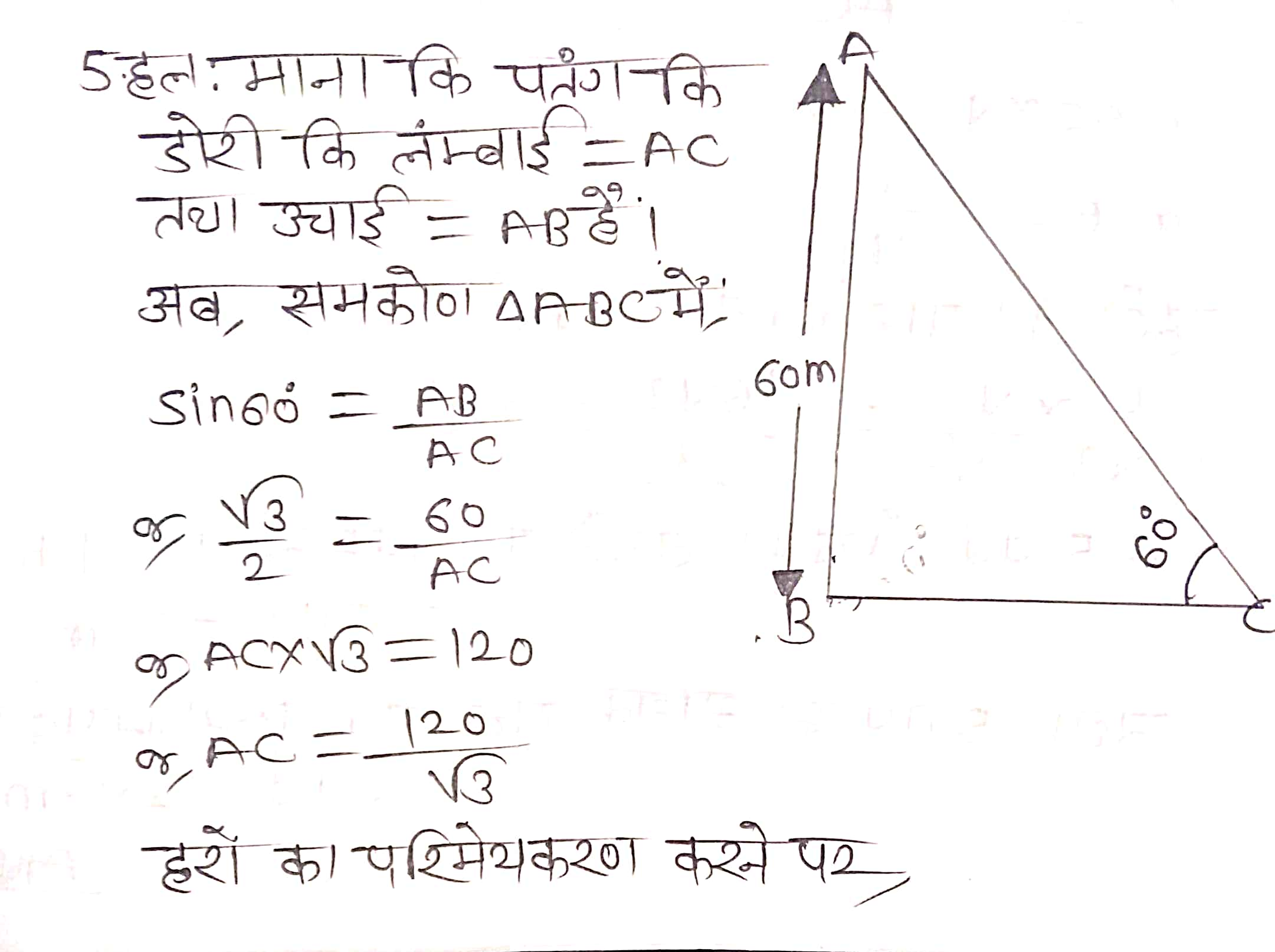
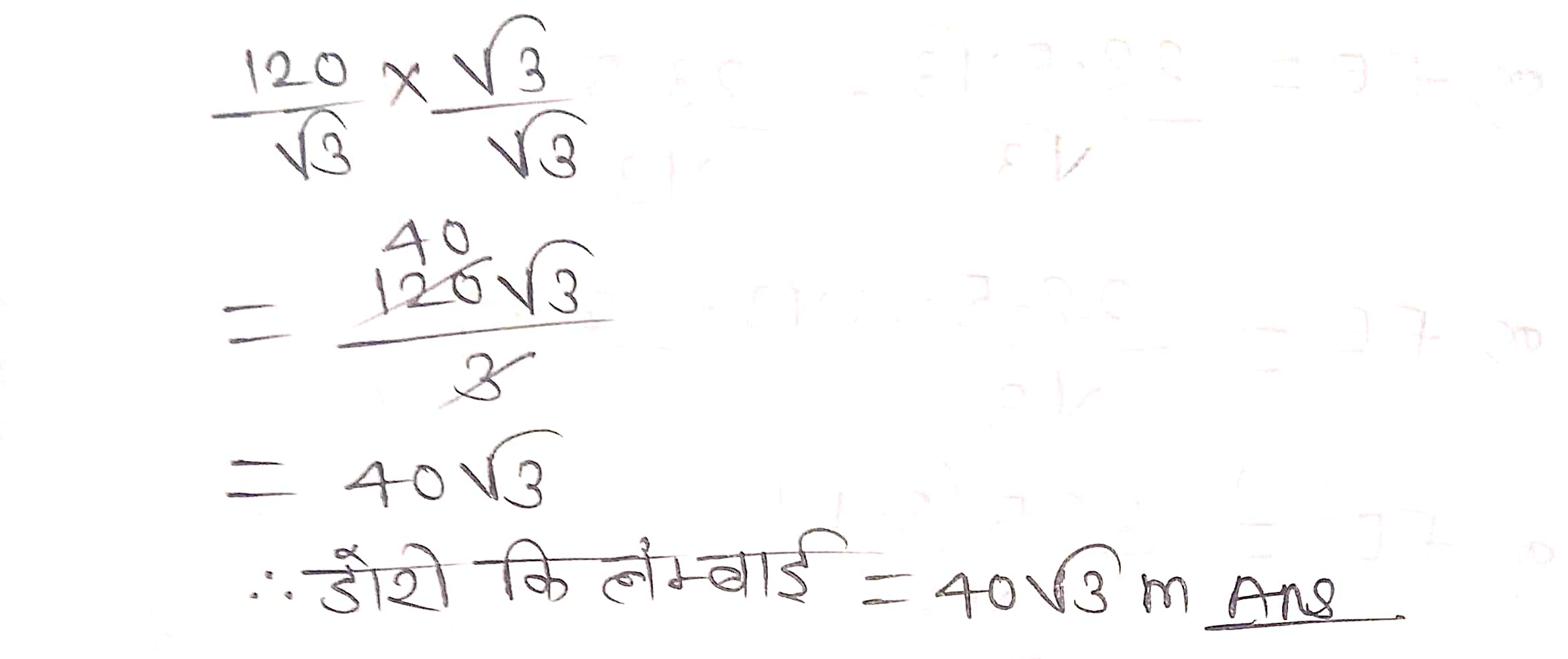
प्रश्न 6. 1.5 m लम्बा एक लड़का 30 m ऊँचे एक भवन से कुछ दूरी पर खड़ा है। जब वह ऊँचे भवन की ओर जाता है तब उसकी आँख से भवन के शिखर का उन्नयन कोण 30° से 60° हो जाता है। बताइए कि वह भवन की ओर कितनी दूरी तक चलकर गया है?

 

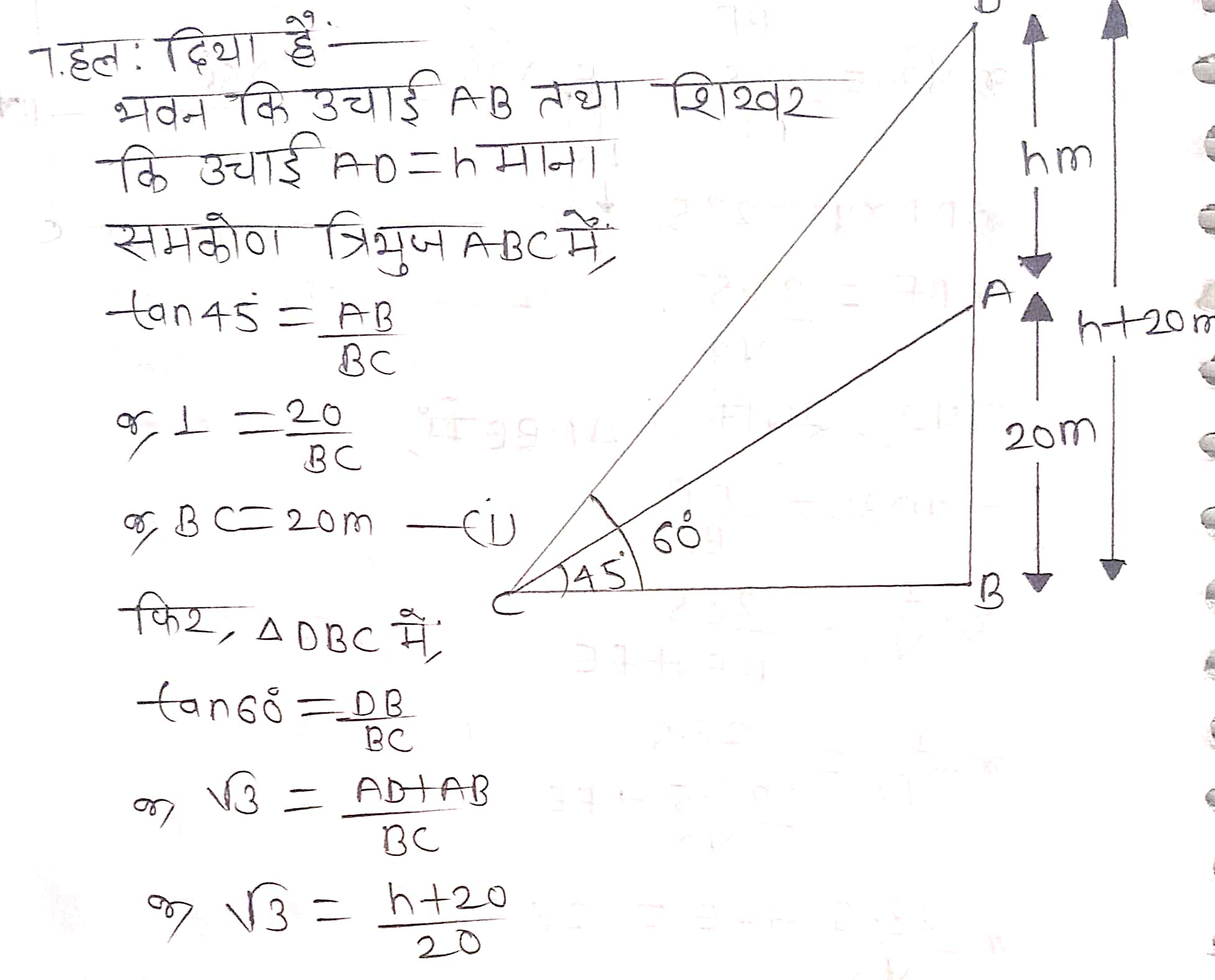
प्रश्न 7. भूमि के एक बिन्दु से एक 20 m ऊँचे भवन के शिखर पर लगी एक संचार मीनार के तल और शिखर के उन्नयन कोण क्रमशः 45° और 60° हैं। मीनार की ऊँचाई ज्ञात कीजिए।

 

प्रश्न 8. एक पेडस्टल के शिखर पर एक 1.6 m ऊँची मूर्ति लगी है। भूमि के एक बिन्दु से मूर्ति के शिखर का उन्नयन कोण 60° है और उसी बिन्दु से पेडस्टल के शिखर का उन्नयन कोण 45° है। पेडस्टल की ऊँचाई ज्ञात कीजिए।

 

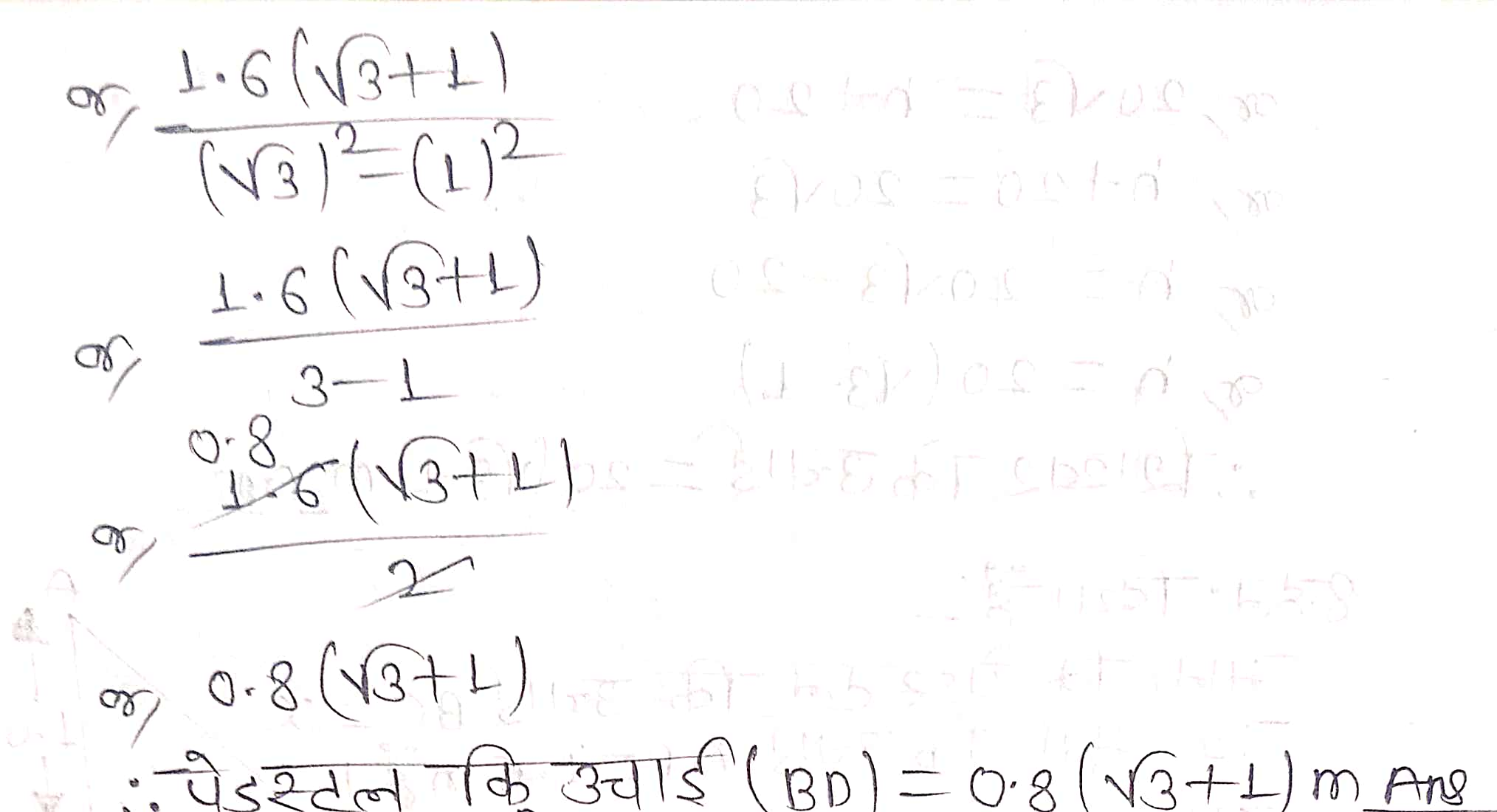
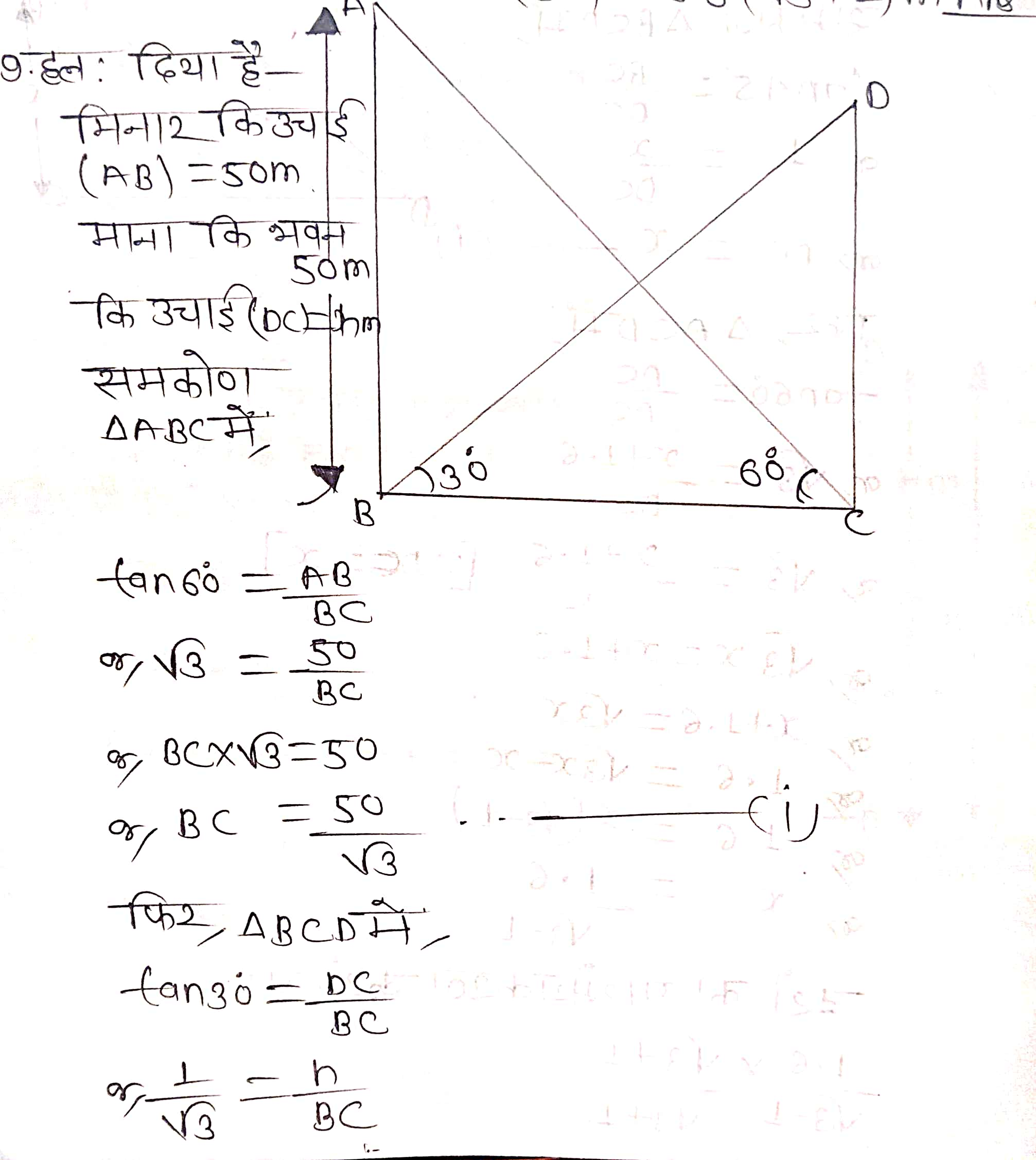
प्रश्न 9. एक मीनार के पाद-बिन्दु से एक भवन के शिखर का उन्नयन कोण 30° है और भवन के पाद-बिन्दु से मीनार के शिखर का उन्नयन कोण 60° है। यदि मीनार 50 m ऊँची हो, तो भवन की ऊँचाई ज्ञात कीजिए।

 

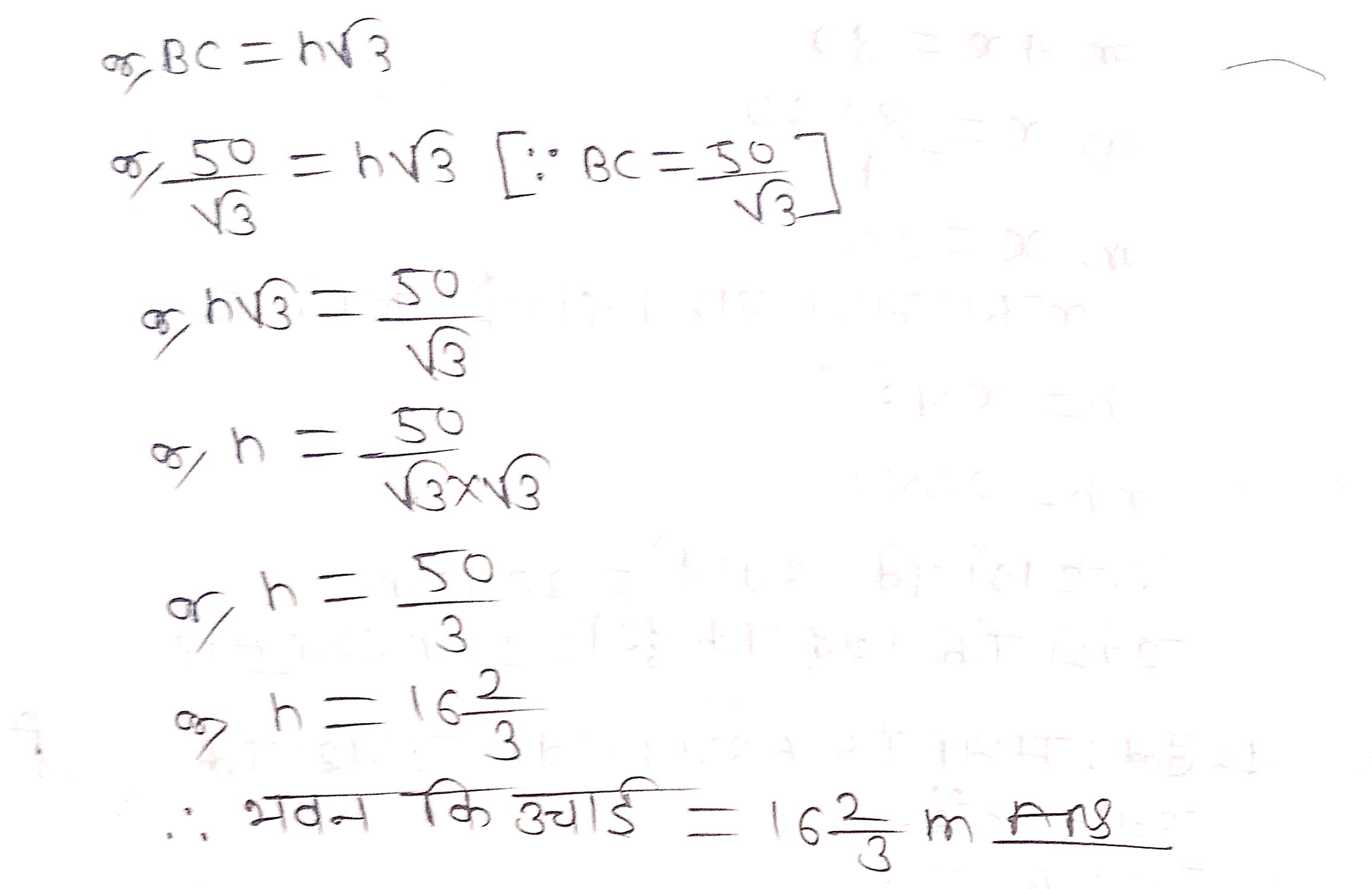
प्रश्न10. एक 80 m चौड़ी सड़क के दोनों ओर आमने-सामने समान ऊँचाई वाले दो खम्भे लगे हुए हैं। इन दोनों खम्भों के बीच सड़क के एक बिन्दु से खम्भों के शिखर के उन्नयन कोण क्रमश: 60° और 30° हैं। खम्भों की ऊँचाई और खम्भों से बिन्द की दूरी ज्ञात कीजिए।

 

प्रश्न 11. एक नहर के एक तट पर एक टीवी टॉवर ऊर्ध्वाधरतः खड़ा है। टॉवर के ठीक सामने दूसरे तट के एक अन्य बिन्दु से टॉवर के शिखर का उन्नयन कोण 60° है। इसी तट पर इस बिन्दु से 20 m दूर और इस बिन्द को मीनार के पाद से मिलाने वाली रेखा पर स्थित एक अन्य बिन्द से टॉवर के शिखर का उन्नयन कोण 30° है (चित्र देखिए)। टॉवर की ऊँचाई और नहर की चौड़ाई ज्ञात कीजिए।

 

प्रश्न 12. 7 m ऊँचे भवन के शिखर से एक केबल टॉवर के शिखर का उन्नयन कोण 60° है और इसके पाद का अवनमन कोण 45° है। टॉवर की ऊँचाई ज्ञात कीजिए।

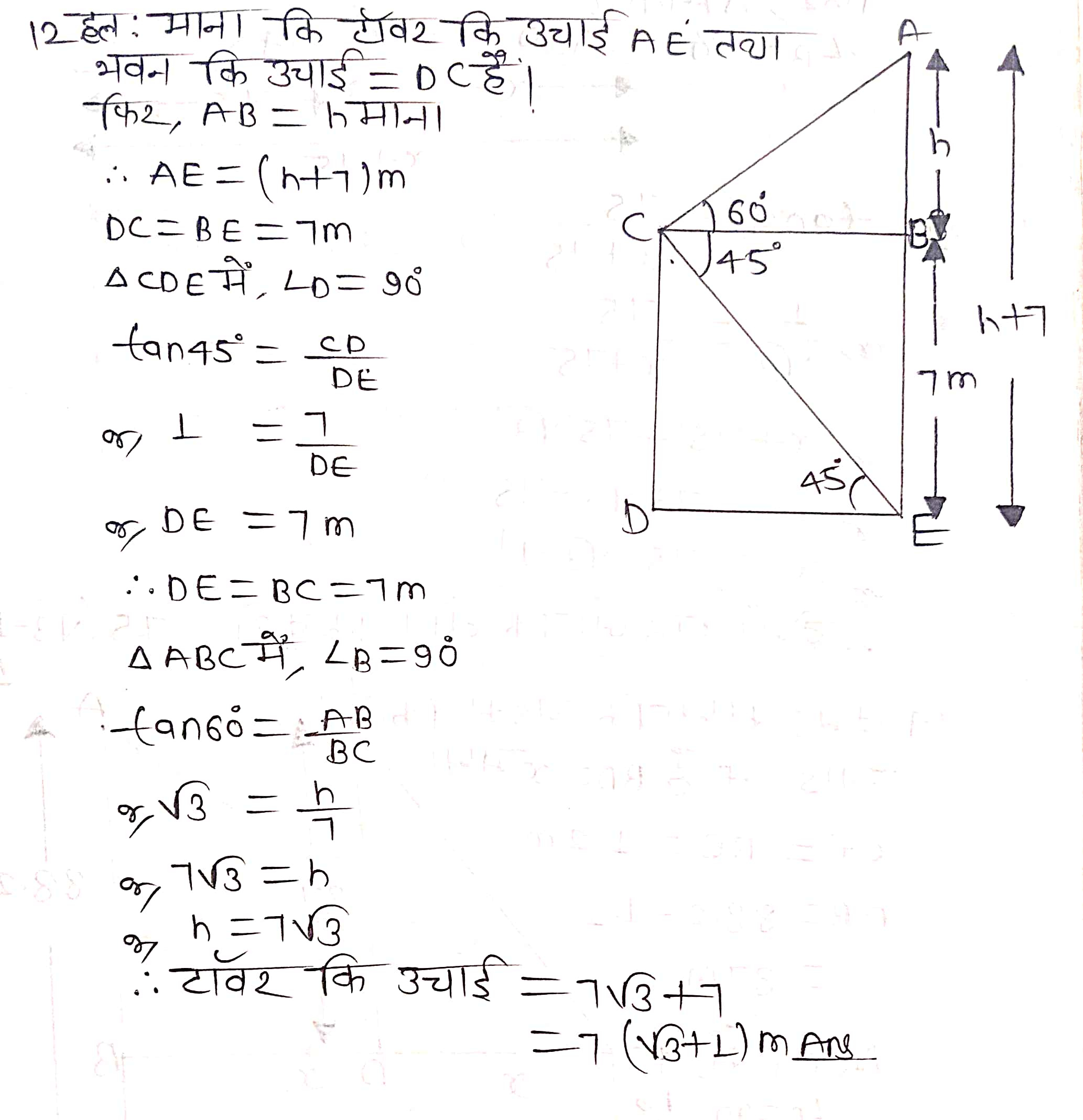
प्रश्न 13. समुद्र-तल से 75 m ऊँची लाइट हाउस के शिखर से देखने पर दो समुद्री जहाजों के अवनमन कोण 30° और 45° हैं। यदि लाइट हाउस के एक ही ओर एक जहाज दूसरे जहाज के ठीक पीछे हो तो दो जहाजों के बीच की दूरी ज्ञात कीजिए।

प्रश्न 14. 1.2 m लम्बी एक लड़की भूमि से 88.2 m की ऊँचाई पर एक क्षैतिज रेखा में हवा में उड़ रहे गुब्बारे को देखती है। किसी भी क्षण लड़की की आँख से गुब्बारे का उन्नयन कोण 60° है। कुछ समय बाद उन्नयन कोण घटकर 30° हो जाता है। इस अन्तराल के दौरान गुब्बारे द्वारा तय की गई दूरी ज्ञात कीजिए।

 

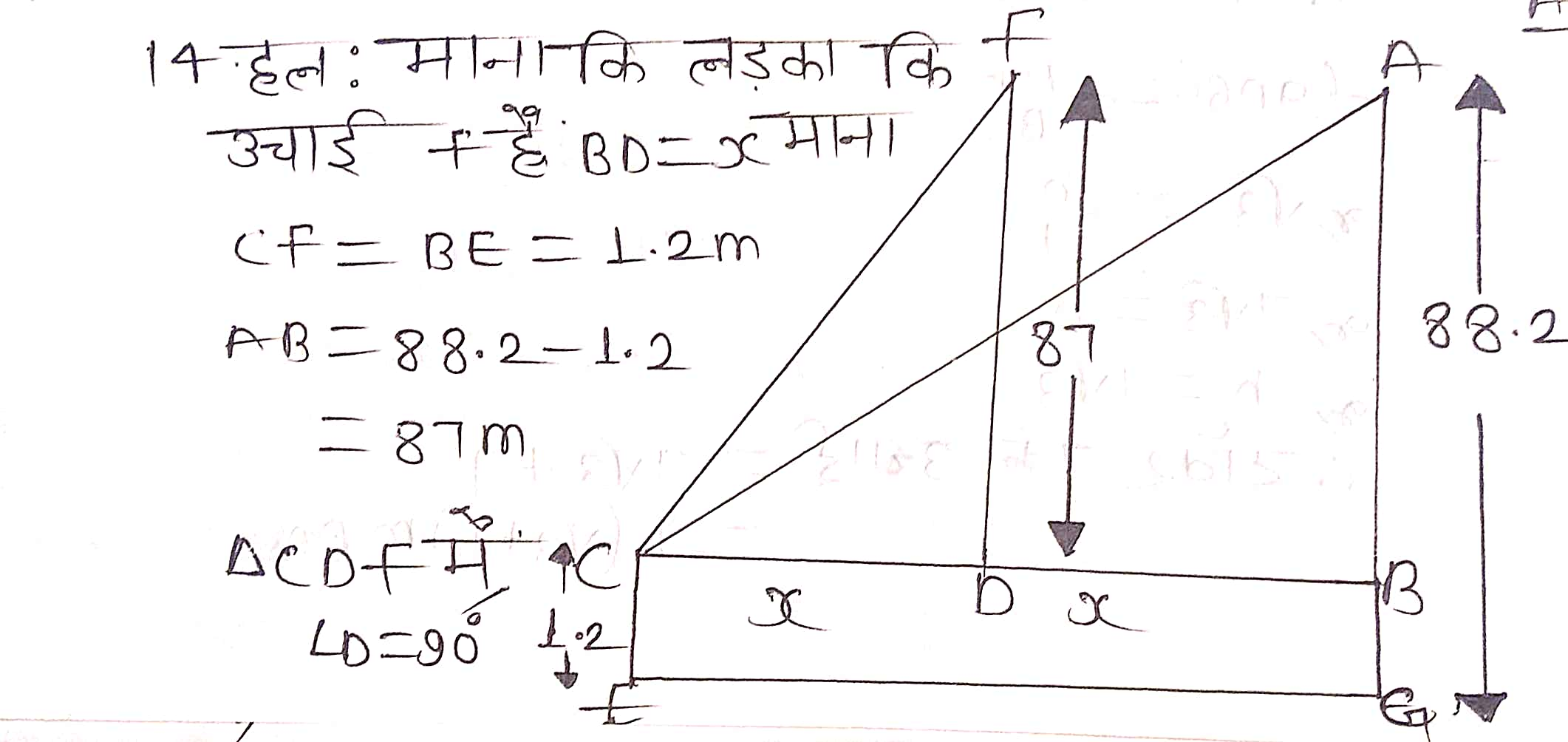
प्रश्न 15. एक सीधा राजमार्ग एक मीनार के पाद तक जाता है। मीनार के शिखर पर खड़ा एक आदमी एक कार को 30° के अवनमन कोण पर देखता है जो कि मीनार के पाद की ओर एकसमान चाल से जाता है। छ: सेकण्ड बाद कार का अवनमन कोण 60° हो गया। इस बिन्दु से मीनार के पाद तक पहुँचने में कार द्वारा लिया गया समय ज्ञात कीजिए।

  

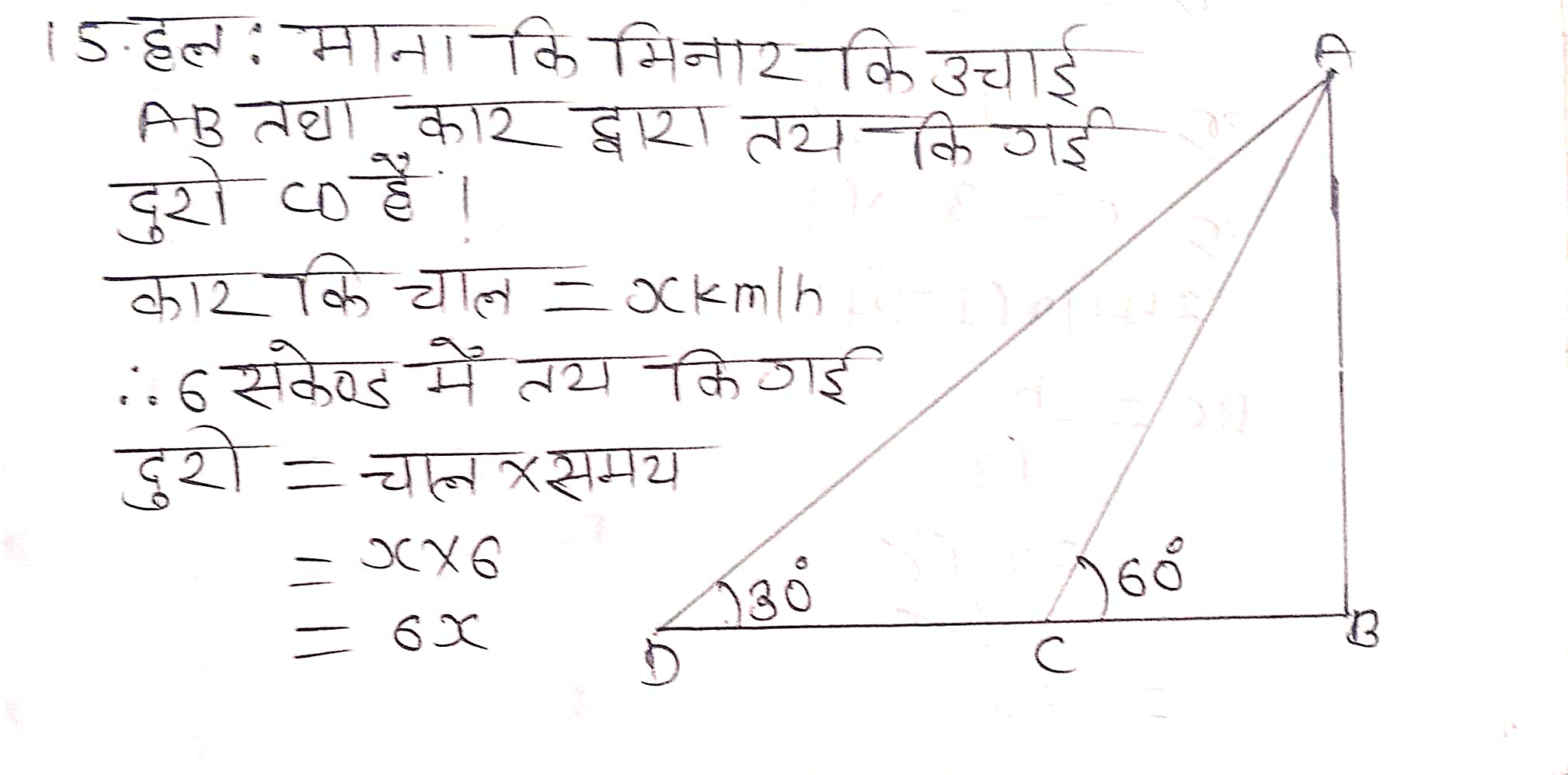
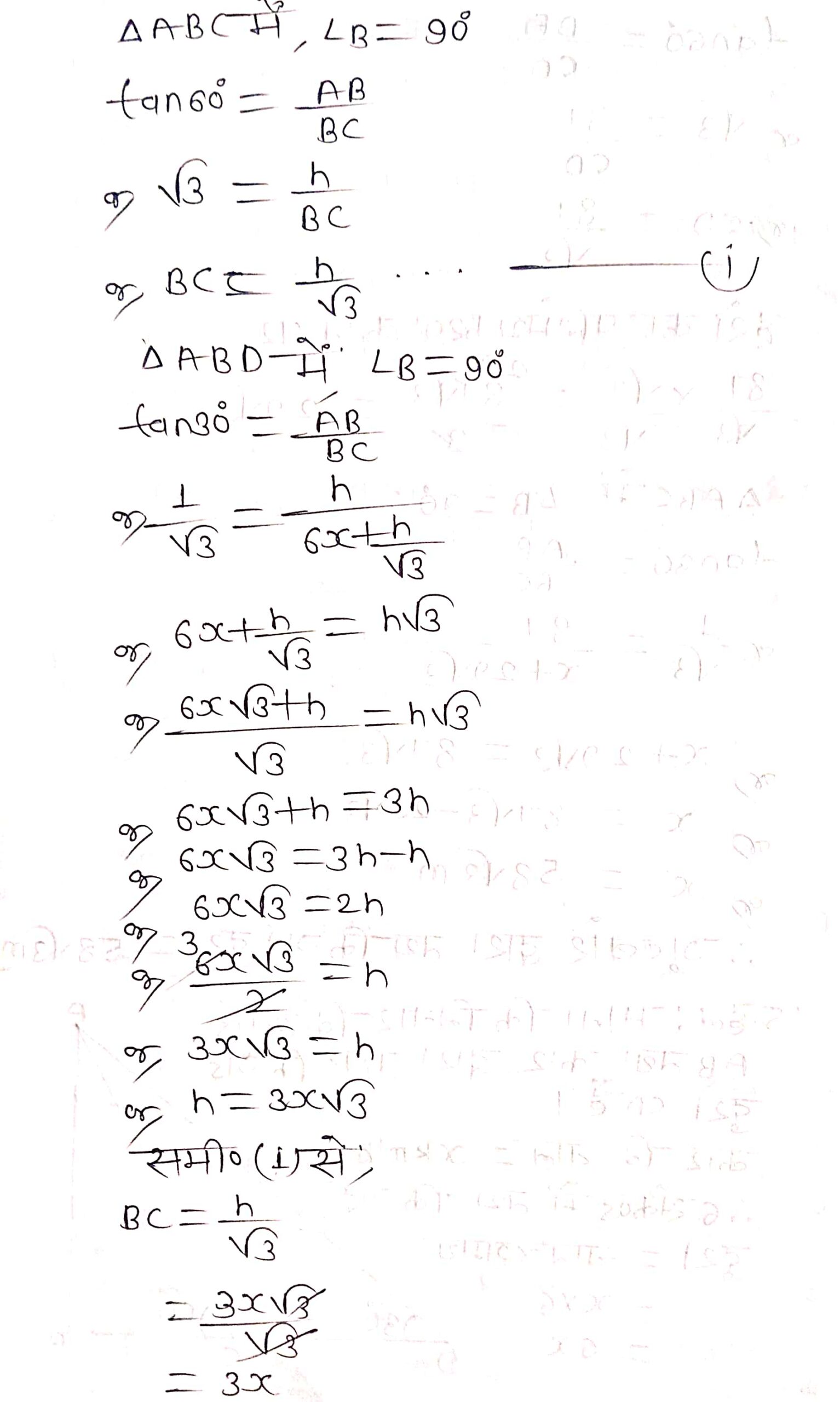
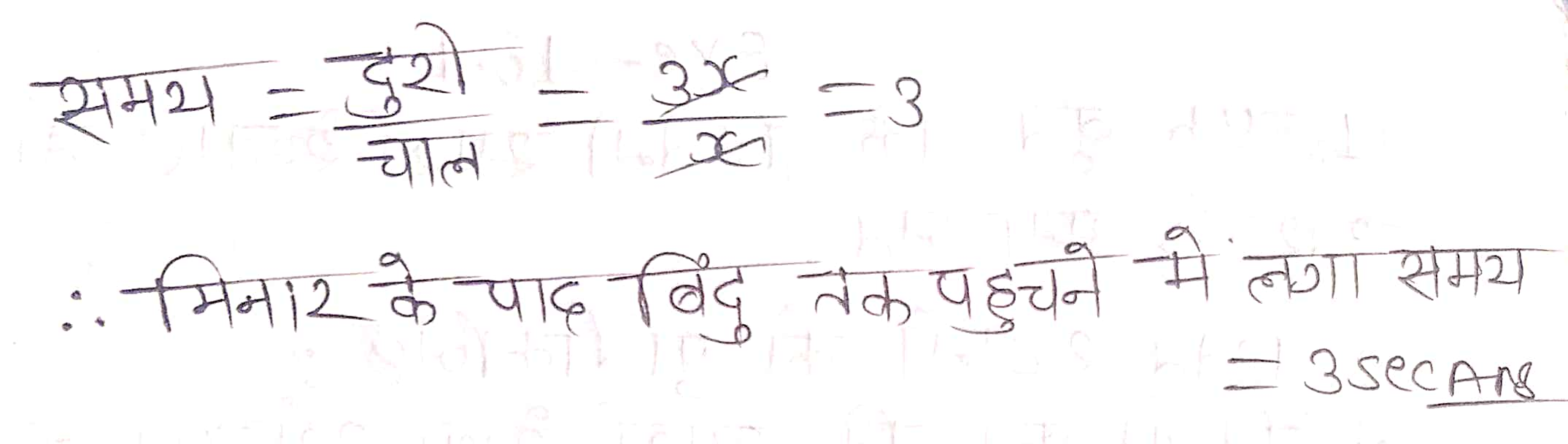
प्रश्न 16. मीनार के आधार से और एक सरल रेखा में 4 m और 9 m की दूरी पर स्थित दो बिन्दुओं से मीनार के शिखर के उन्नयन कोण पूरक कोण हैं। सिद्ध कीजिए कि मीनार की ऊँचाई 6 m है।